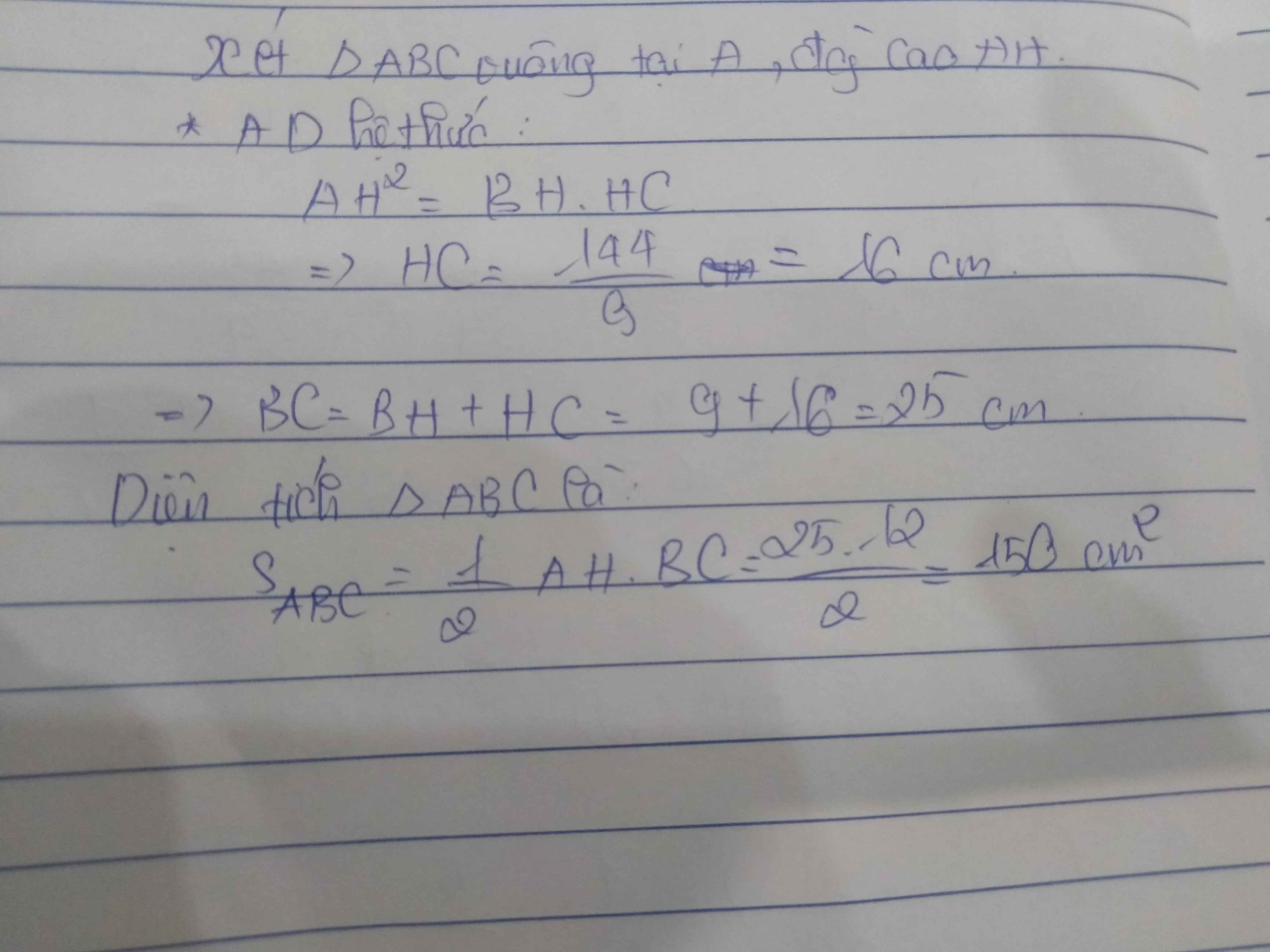Bài 5: 

Ta có: \(AB^2=BH\cdot BC\)

\(\Leftrightarrow BH\left(BH+9\right)=400\)

\(\Leftrightarrow BH^2+25HB-16HB-400=0\)

\(\Leftrightarrow BH=16\left(cm\right)\)

hay BC=25(cm)

Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

Lời giải:

$BC=BH+CH=25+64=89$ (cm)

Áp dụng công thức hệ thức lượng trong tam giác vuông:

$AH^2=BH.CH=25.64\Rightarrow AH=40$ (cm)

Diện tích tam giác $ABC$ là: $AH.BC:2=40.89:2=1780$ (cm²)

Áp dụng HTL trong tam giác vuông ABC : 

\(AH^2=BH\cdot CH\)

\(\Rightarrow CH=\dfrac{12^2}{9}=16\left(cm\right)\)

\(BC=BH+CH=9+16=25\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}\cdot12\cdot25=150\left(cm^2\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH^2=HB\cdot HC\)

\(\Leftrightarrow HC=\dfrac{AH^2}{HB}=\dfrac{12^2}{9}=16\left(cm\right)\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=150\left(cm^2\right)\)

Tính được  S A B C = 150 c m 2

Mấy bài này cũng easy thôi

a) \(\Delta ABC;\widehat{A}=1v\left(gt\right)\)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}\)\(=20\left(cm\right)\)

Tam giác ABC đồng dạng với tam giác HBA ( \(\widehat{B}\)chung \(\widehat{BAC}=\widehat{BAH}=90^0\))

\(\Rightarrow\frac{AB}{BH}=\frac{AC}{AH}=\frac{BC}{AB}\)

hay \(\frac{12}{BH}=\frac{16}{AH}=\frac{20}{12}=\frac{10}{6}\)

\(\Rightarrow AH=\frac{16.6}{10}=9,6\left(cm\right)\)

\(\Rightarrow BH=\frac{12.6}{10}=7,2\left(cm\right)\)

\(\Rightarrow HC=BC-BH=20-7,2=12,8\)( cm )

b) \(\Delta HMA\)vuông tại H

\(\Rightarrow S_{HMA}=\frac{1}{2}HM.AH\)\(=\frac{1}{2}.2,8.9,6=13,44\left(cm^2\right)\)

Áp dụng định lí Py-ta-go cho  \(\Delta AHC\) vuông tại H ta được :

\(HC^2=AC^2-AH^2\)

\(\Leftrightarrow HC^2=20^2-12^2\)

\(\Leftrightarrow HC^2=256\)

\(\Leftrightarrow HC=16\left(cm\right)\)

Áp dụng hệ thức lượng ta được : \(AH^2=HC.HB\)

\(\Leftrightarrow12^2=BH.16\)

\(\Leftrightarrow BH=9\left(cm\right)\)

Ta có :  \(S_{\Delta ABC}=\frac{AH.BC}{2}=\frac{AH.\left(BH+CH\right)}{2}=\frac{12\left(9+16\right)}{2}=\frac{300}{2}=150\left(cm^2\right)\)

Vậy  \(S_{\Delta ABC}=150cm^2\)

Xét ΔABC vuông tại A và ΔHAC vuông tại H có

góc C chung

=>ΔABC đồng dạng với ΔHAC

BA^2=HB*HC

=>HB(HB+10,8)=7,2^2

=>HB^2+10,8HB-7,2^2=0

=>HB=3,6cm

=>BC=14,4cm

\(AC=\sqrt{14.4^2-7.2^2}=\dfrac{36}{5}\sqrt{3}\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}\cdot\dfrac{36\sqrt{3}}{5}\cdot7.2\simeq44,89\left(cm^2\right)\)

Áp dụng HTL:

\(AH^2=BH.HC\)

\(\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{12^2}{9}=16\left(cm\right)\)

\(\Rightarrow BC=BH+HC=16+9=25\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.12.25=150\left(cm^2\right)\)