\(\left[{}\begin{matrix}13123\\435\\12432\\65467556\end{matrix}\right.\)
hãy tính kết quả
Những câu hỏi liên quan
Giải các hệ phương trình sau bằng máy tính bỏ túi (làm tròn kết quả dến chữ số thập phân thứ hai)
a. left{{}begin{matrix}3x-5y64x+7y-8end{matrix}right.
b. left{{}begin{matrix}-2x+3y55x+2y4end{matrix}right.
c. left{{}begin{matrix}2x-3y+4z-5-4x+5y-z63x+4y-3z7end{matrix}right.
d. left{{}begin{matrix}-x+2y-3z22x+y+2z-3-2x-3y+z5end{matrix}right.
Đọc tiếp
Giải các hệ phương trình sau bằng máy tính bỏ túi (làm tròn kết quả dến chữ số thập phân thứ hai)
a. \(\left\{{}\begin{matrix}3x-5y=6\\4x+7y=-8\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}-2x+3y=5\\5x+2y=4\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}2x-3y+4z=-5\\-4x+5y-z=6\\3x+4y-3z=7\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}-x+2y-3z=2\\2x+y+2z=-3\\-2x-3y+z=5\end{matrix}\right.\)
a. \(\left\{{}\begin{matrix}3x-5y=6\\4x+7y=-8\end{matrix}\right.\)
\(x=\dfrac{2}{41}\) ; \(y=\dfrac{-48}{41}\)
b. \(\left\{{}\begin{matrix}\text{−2x+3y=5}\\5x+2y=4\end{matrix}\right.\)
\(x=\dfrac{2}{19};y=\dfrac{33}{19}\)
c.\(\left\{{}\begin{matrix}\text{2x−3y+4z=−5}\\-4x+5y-z=6\\3x+4y-3z=7\end{matrix}\right.\)
\(x=\dfrac{22}{101};y=\dfrac{131}{101};z=\dfrac{-39}{101}\)
d. \(\left\{{}\begin{matrix}\text{− x + 2 y − 3 z = 2}\\2x+y+2z=-3\\-2x-3y+z=5\end{matrix}\right.\)
\(x=-4;y=\dfrac{11}{7};z=\dfrac{12}{7}\)
Đúng 0
Bình luận (1)
a)x=0,05 ; y=-1,17
b.x=0,11 ; y=1,74
c.x=0,22 ;y=1,29 z=-0.39
d.x=-4 y=1,57 z=1,71
Đúng 0
Bình luận (0)
a,\(\left\{{}\begin{matrix}3x-5y=6\\4x+7y=-8\end{matrix}\right.\)
x=\(\dfrac{2}{41}=0,05\) ; y=\(\dfrac{-48}{41}=-1,17\)
b,\(\left\{{}\begin{matrix}-2x+3y=5\\5x+2y=4\end{matrix}\right.\)
x=\(\dfrac{2}{19}=0,11\) ; y=\(\dfrac{33}{19}=1,74\)
c,\(\left\{{}\begin{matrix}2x-3y+4z=-5\\-4x+5y-z=6\\3x+4y-3z=2\end{matrix}\right.\)
x=\(\dfrac{22}{101}=0,22\) ;y=\(\dfrac{131}{101}=1,29\) ; z=\(\dfrac{-39}{101}=-0,39\)
d,\(\left\{{}\begin{matrix}-x+2y-3z=2\\2x+y+2z=-3\\-2x-3y+z=5\end{matrix}\right.\)
x=\(-4\) ; y=\(\dfrac{11}{7}=1,57\) ; z=\(\dfrac{12}{7}=1,71\)
Đúng 0
Bình luận (0)
bằng trục số hãy tìm x thỏa mãn:
1.left{{}begin{matrix}x 5left[{}begin{matrix}x -2x1end{matrix}right.end{matrix}right.
2.left{{}begin{matrix}x0left[{}begin{matrix}x1x 0end{matrix}right.end{matrix}right.
3.left[{}begin{matrix}left{{}begin{matrix}x1x 5end{matrix}right.x -2end{matrix}right.
4.left[{}begin{matrix}x2left{{}begin{matrix}x 5x-2end{matrix}right.end{matrix}right.
Đọc tiếp
bằng trục số hãy tìm x thỏa mãn:
1.\(\left\{{}\begin{matrix}x< 5\\\left[{}\begin{matrix}x< -2\\x>1\end{matrix}\right.\end{matrix}\right.\)
2.\(\left\{{}\begin{matrix}x>0\\\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\end{matrix}\right.\)
3.\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x>1\\x< 5\end{matrix}\right.\\x< -2\\\end{matrix}\right.\)
4.\(\left[{}\begin{matrix}x>2\\\left\{{}\begin{matrix}x< 5\\x>-2\end{matrix}\right.\\\end{matrix}\right.\)
1: \(x\in\left(1;5\right)\cup\left(-\infty;-2\right)\)
2: x>1
4: \(x\in\left(-2;+\infty\right)\)
Đúng 0
Bình luận (0)
Giải hệ phương trình
left{{}begin{matrix}x^2+y^2+xy13x^4+y^4+x^2y^291end{matrix}right.
Leftrightarrowleft{{}begin{matrix}left(x+yright)^2-xy13left(x^2+y^2right)^2-left(xyright)^291end{matrix}right.
Leftrightarrowleft{{}begin{matrix}left(x+yright)^213+xyleft[left(x+yright)^2-2xyright]^2-left(xyright)^291end{matrix}right.
Leftrightarrowleft{{}begin{matrix}left(x+yright)^2-xy13left(13-xyright)^2-left(xyright)^291end{matrix}right.
Leftrightarrowleft{{}begin{matrix}xy3left(x+yright)^216end{matri...
Đọc tiếp
Giải hệ phương trình
\(\left\{{}\begin{matrix}x^2+y^2+xy=13\\x^4+y^4+x^2y^2=91\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2-xy=13\\\left(x^2+y^2\right)^2-\left(xy\right)^2=91\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2=13+xy\\\left[\left(x+y\right)^2-2xy\right]^2-\left(xy\right)^2=91\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2-xy=13\\\left(13-xy\right)^2-\left(xy\right)^2=91\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=3\\\left(x+y\right)^2=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=4\\xy=3\end{matrix}\right.\) hoặc x+y = -4
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+y=4\\xy=3\end{matrix}\right.\\\left\{{}\begin{matrix}x+y=-4\\xy=3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-3\\y=-1\end{matrix}\right.\end{matrix}\right.\)hoặc \(\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)hoặc \(\left\{{}\begin{matrix}x=-1\\y=-3\end{matrix}\right.\)
Mọi người có thể giải thích từ dấu tương đương thứ 3 xuống 4. tại sao lại như vậy k?
Thu gọn các hệ điều kiện sau:
a/ left{{}begin{matrix}xin(-1;3]xinleft(-infty;2right)cupleft(4;+inftyright)end{matrix}right.
b/left{{}begin{matrix}8le xle30left[{}begin{matrix}x 10xge25end{matrix}right.end{matrix}right.
c/left{{}begin{matrix}left[{}begin{matrix}x -2x4end{matrix}right.left[{}begin{matrix}x -5xge7end{matrix}right.end{matrix}right.
Đọc tiếp
Thu gọn các hệ điều kiện sau:
a/ \(\left\{{}\begin{matrix}x\in(-1;3]\\x\in\left(-\infty;2\right)\cup\left(4;+\infty\right)\end{matrix}\right.\)
b/\(\left\{{}\begin{matrix}8\le x\le30\\\left[{}\begin{matrix}x< 10\\x\ge25\end{matrix}\right.\end{matrix}\right.\)
c/\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x< -2\\x>4\end{matrix}\right.\\\left[{}\begin{matrix}x< -5\\x\ge7\end{matrix}\right.\end{matrix}\right.\)
a: \(x\in\left(-1;2\right)\)
b: \(x\in[8;10)\cup\left[25;30\right]\)
c: \(x\in\left(-\infty;-5\right)\cup[7;+\infty)\)
Đúng 0
Bình luận (0)
Trên quả Địa Cầu, hãy tìm các điểm có toạ độ địa lí sau:
\(\left\{{}\begin{matrix}80^{\text{o}}\text{Đ}\\30^{\text{o}}N\end{matrix}\right.\)
\(\left\{{}\begin{matrix}60^{\text{o}}T\\40^{\text{o}}N\end{matrix}\right.\)
Trên quả Địa cầu, các điểm có toạ độ địa lí:
\(\left\{{}\begin{matrix}80^0Đ\\30^0N\end{matrix}\right.\) là toạ độ của một địa điểm ở giữa Ấn Độ Dương.
\(\left\{{}\begin{matrix}60^0T\\40^0N\end{matrix}\right.\) là toạ độ của một địa điểm thuộc vùng biển phía Đông Ác-hen-ti-na.
Đúng 0
Bình luận (0)
\(\left\{{}\begin{matrix}x+y=19\\xy+6x=150\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=19-y\\x\left(y+6\right)=150\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=19-y\\\left(19-y\right)\left(y+6\right)=150\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=19-9=10\\y=9\end{matrix}\right.\)
Cho biết tình hình nông nghiệp của các nước châu Á
a)Trồng trọt : - Cây lương thực left{{}begin{matrix}end{matrix}right.
- Cây công nghiệpleft{{}begin{matrix}end{matrix}right.
- Cây ăn quả và cây khácleft{{}begin{matrix}end{matrix}right.
b) Chăn nuôi : - Gia súc lớnleft{{}begin{matrix}end{matrix}right.
- Gia súc nhỏleft{{}begin{matrix}end{matrix}right.
- Gia cầmleft{{}begin{matrix}end{matrix}right...
Đọc tiếp
Cho biết tình hình nông nghiệp của các nước châu Á
a)Trồng trọt : - Cây lương thực \(\left\{{}\begin{matrix}\\\\\end{matrix}\right.\)
- Cây công nghiệp\(\left\{{}\begin{matrix}\\\\\\\end{matrix}\right.\)
- Cây ăn quả và cây khác\(\left\{{}\begin{matrix}\\\\\end{matrix}\right.\)
b) Chăn nuôi : - Gia súc lớn\(\left\{{}\begin{matrix}\\\\\\\end{matrix}\right.\)
- Gia súc nhỏ\(\left\{{}\begin{matrix}\\\\\\\end{matrix}\right.\)
- Gia cầm\(\left\{{}\begin{matrix}\\\\\\\end{matrix}\right.\)
Giải các hệ phương trình sau và minh họa hình học kết quả tìm được:
a) \(\left\{{}\begin{matrix}2x+5y=2\\\dfrac{2}{5}x+y=1\end{matrix}\right.;\)
b) \(\left\{{}\begin{matrix}0,2x+0,1y=0,3\\3x+y=5\end{matrix}\right.;\)
c) \(\left\{{}\begin{matrix}\dfrac{3}{2}x-y=\dfrac{1}{2}\\3x-2y=1\end{matrix}\right..\)
a) Giải hệ phương trình:
{2x+5y=2(1)25x+y=1(2)⇔{2x+5y=2(1′)−2x−5y=−5(2′){2x+5y=2(1)25x+y=1(2)⇔{2x+5y=2(1′)−2x−5y=−5(2′)
Cộng (1’) với (2’) vế theo vế, ta được: 0x + 0y = -3
Phương trình này vô nghiệm. Vậy hệ đã cho vô nghiệm.
Minh họa hình học kết quả tìm được:
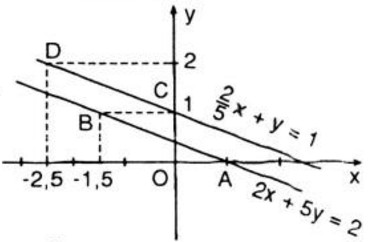
- Vẽ đồ thị hàm số 2x + 5y = 2.
Cho y = 0 ⇒ x = 1. Ta xác định được điểm A(1; 0)
Cho y = 1 ⇒ x = -1,5. Ta xác định được điểm B(-1,5; 1).
Đồ thị hàm số là đường thẳng đi qua hai điểm A và B
-Vẽ đồ thị hàm số 25x+y=1⇔2x+5y=525x+y=1⇔2x+5y=5
Cho x = 0 ⇒ y = 1. Ta xác định được điểm C(0; 1)
Cho y = 2 ⇒ x = -2,5. Ta xác định được điểm D(-2,5; 2)
Đồ thị hàm số là đường thẳng đi qua hai điểm C và D.
Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm.
b) Giải hệ phương trình:
{0,2x+0,1y=0,3(1)3x+y=5(2)⇔{−2x−y=−3(1′)3x+y=5(2′){0,2x+0,1y=0,3(1)3x+y=5(2)⇔{−2x−y=−3(1′)3x+y=5(2′)
Cộng (1’) với (2’) vế theo vế, ta được x = 2
Thế x = 2 vào (2), ta được: 6 + y = 5 ⇔ y = -1
Vậy nghiệm của hệ phương trình là (x = 2; y = -1)
Minh họa hình học:
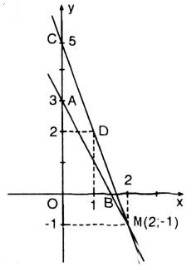
- Đồ thị hàm số 0,2x + 0,1y = 0,3 là một đường thẳng đi qua hai điểm:
A(x = 0; y = 3) và B(x = 1,5; y = 0)
- Đồ thị hàm số 3x + y = 5 là một đường thẳng đi qua hai điểm C(x = 0; y = 5) và D(x = 1; y = 2)
- Đồ thị hai hàm số trên cắt nhau tại điểm: M(x = 2; y = -1).
Vậy (2; -1) là một nghiệm của hệ phương trình.
c) Giải hệ phương trình:
{32x−y=12(1)3x−2y=1(2)⇔{−3x+2y=−1(1′)3x−2y=1(2′){32x−y=12(1)3x−2y=1(2)⇔{−3x+2y=−1(1′)3x−2y=1(2′)
Cộng (1’) và (2’) vế theo vế, ta có: 0x + 0y = 0.
Phương trình này có vô số nghiệm.
Nghiệm tổng quát là (x;32x−12)(x;32x−12) với x ∈ R
Minh họa hình học
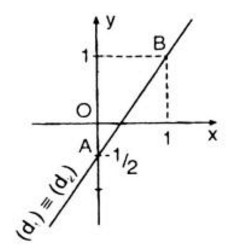
- Đồ thị hàm số (1) là đường thẳng đi qua hai điểm A(0; −12−12) và B(1;1) nên hai đường thẳng này trùng nhau. Vậy hệ phương trinh có vô số nghiệm.
Đúng 0
Bình luận (0)
tính số hạng đầu \(u_1\) và công sai d của 1 cấp số cộng biết
a) \(\left\{{}\begin{matrix}u_4=4\\u_6=8\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}u_1-u_3+u_5=10\\u_1+u_6=17\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}u_1+u_2=5\\u_3u_5=91\end{matrix}\right.\)
a: u4=4 và u6=8
=>u1+3d=4 và u1+5d=8
=>-2d=-4 và u1+3d=4
=>d=2 và u1=4-3d=-2
b: u1-u3+u5=10 và u1+u6=17
=>u1-u1-2d+u1+4d=10 và u1+u1+5d=17
=>u1+2d=10 và 2u1+5d=17
=>u1=16 và d=-3
c: u1+u2=5 và u3*u5=91
=>u1+u1+d=5 và (u1+2d)(u1+4d)=91
=>2u1+d=5 và (u1+2d)(u1+4d)=91
=>d=5-2u1 và (u1+10-4u1)(u1+20-8u1)=91
=>d=5-2u1 và (-3u1+10)(-7u1+20)=91
(-3u1+10)(-7u1+20)=91
=>21u1^2-60u1-70u1+200=91
=>21u1^2-130u1+109=0
=>u1=1 hoặc u1=109/21
Khi u1=1 thì d=5-2u1=5-2=3
Khi u1=109/21 thì d=5-2u1=5-218/21=-113/21
Đúng 0
Bình luận (0)