LM HỘ MÌNH Ý C AH
MÌNH CẢM ƠN Ạ
Lm hộ mình bài này ạ
Mình xin cảm ơn
1 A
2 D
3 B
4 C
5 C
II
1 B
2 C
3 C
4 A
5 C
III
1 - B
2 - C
3 - A
4 - E
5 - F
B
6 so
7 or
8 because
9 and
10 more
Lm hộ mình câu 12 với ạ, mình cảm ơn
Câu 11:
Ta có: \(\left(2x-3\right)\left(3x+2\right)-\left(2x-3\right)^2=-18\)
\(\Leftrightarrow6x^2+4x-9x-6-4x^2+12x-9=-18\)
\(\Leftrightarrow2x^2+7x+3=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Ý a,b,c cho mình xin kết quả để đối chiếu thôi ạ. Còn ý d làm rõ hộ mình. Cảm ơn nhiều ạ❤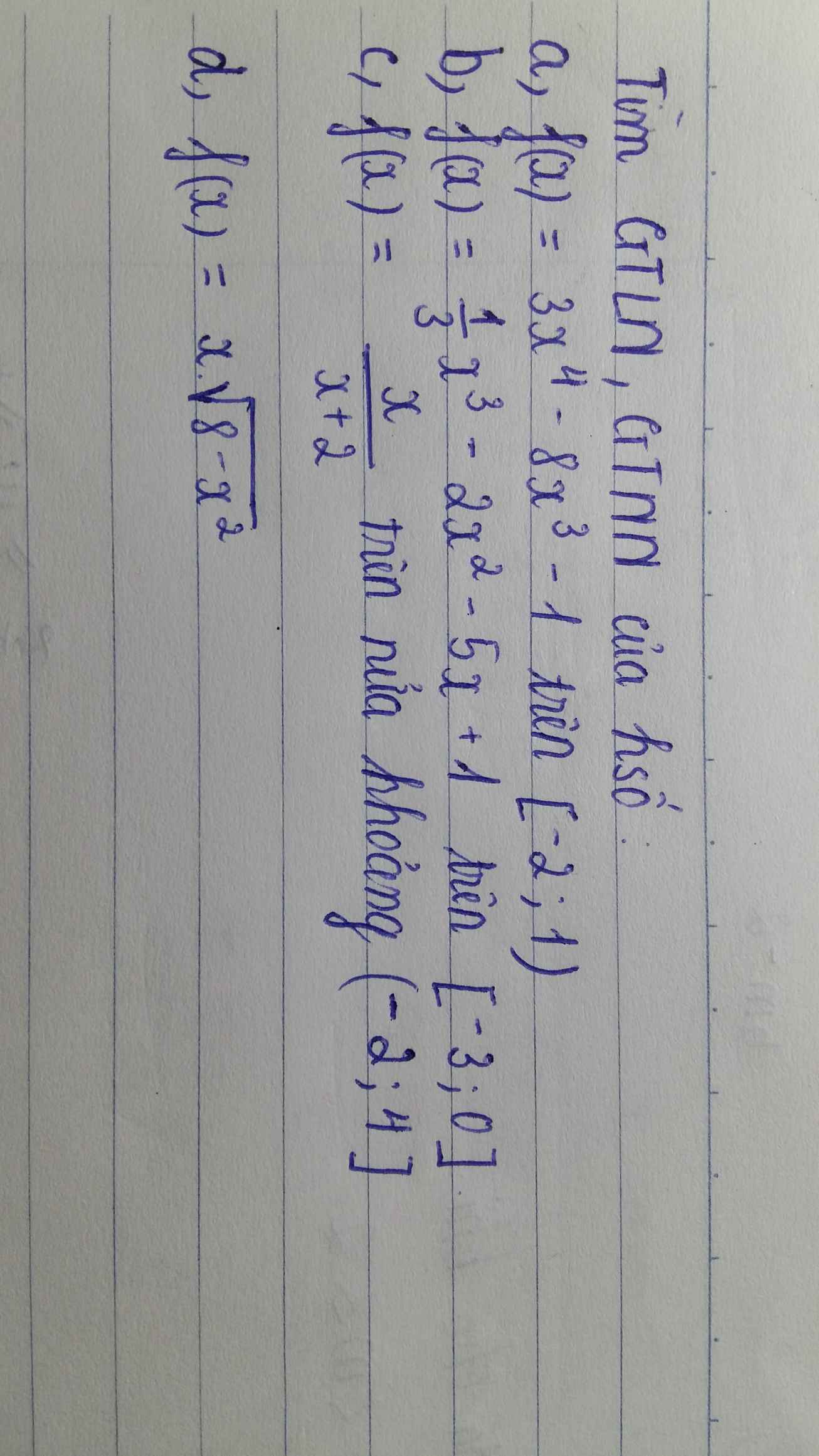
a. \(f\left(x\right)_{max}=f\left(-2\right)=111\) ; \(f\left(x\right)_{min}=f\left(1\right)=-6\)
b. \(f\left(x\right)_{max}=f\left(-3\right)=7\) ; \(f\left(x\right)_{min}=f\left(0\right)=1\)
c. \(f\left(x\right)_{max}=f\left(4\right)=\dfrac{2}{3}\) ; \(f\left(x\right)_{min}\) ko tồn tại
d.
Miền xác định: \(D=\left[-2\sqrt{2};2\sqrt{2}\right]\)
\(y'=\dfrac{2\left(4-x^2\right)}{\sqrt{8-x^2}}=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
\(f\left(-2\sqrt{2}\right)=f\left(2\sqrt{2}\right)=0\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=4\)
\(f\left(x\right)_{max}=f\left(2\right)=4\) ; \(f\left(x\right)_{min}=f\left(-2\right)=-4\)
Bạn nào giải hộ mình 3 ý này với ạ mình cần gấp cảm ơn nhiều ạ
Câu 1:
TXĐ: D=R
\(f\left(-x\right)=2\cdot\left(-x\right)^4-3\cdot\left(-x\right)^2+1=2x^4-3x^2+1=f\left(x\right)\)
Vậy: f(x) là hàm số chẵn
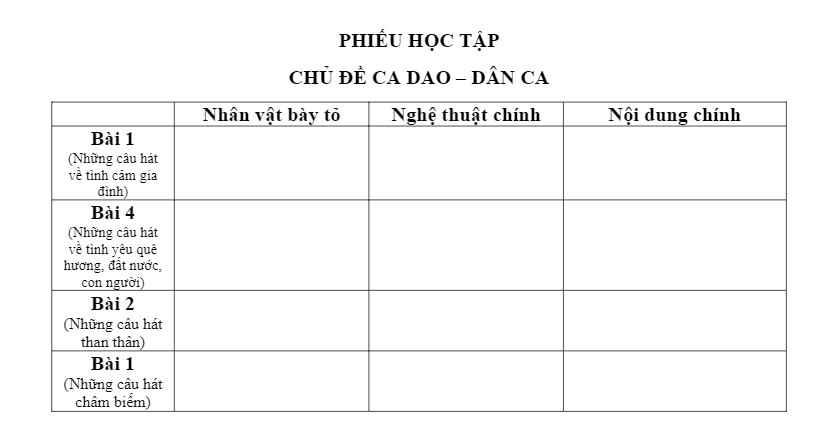
Làm hộ mình để mình có ý tưởng với ạ xin cảm ơn nhiều.
mn lm hộ mk bài 2 với ạ . mk cảm ơn ạ 
Bài 2:
Cả mảnh vải dài:
\(25:\dfrac{3}{5}=\dfrac{125}{3}\left(m\right)\)
Lm hộ mk vs ạ mk cảm ơn 😊
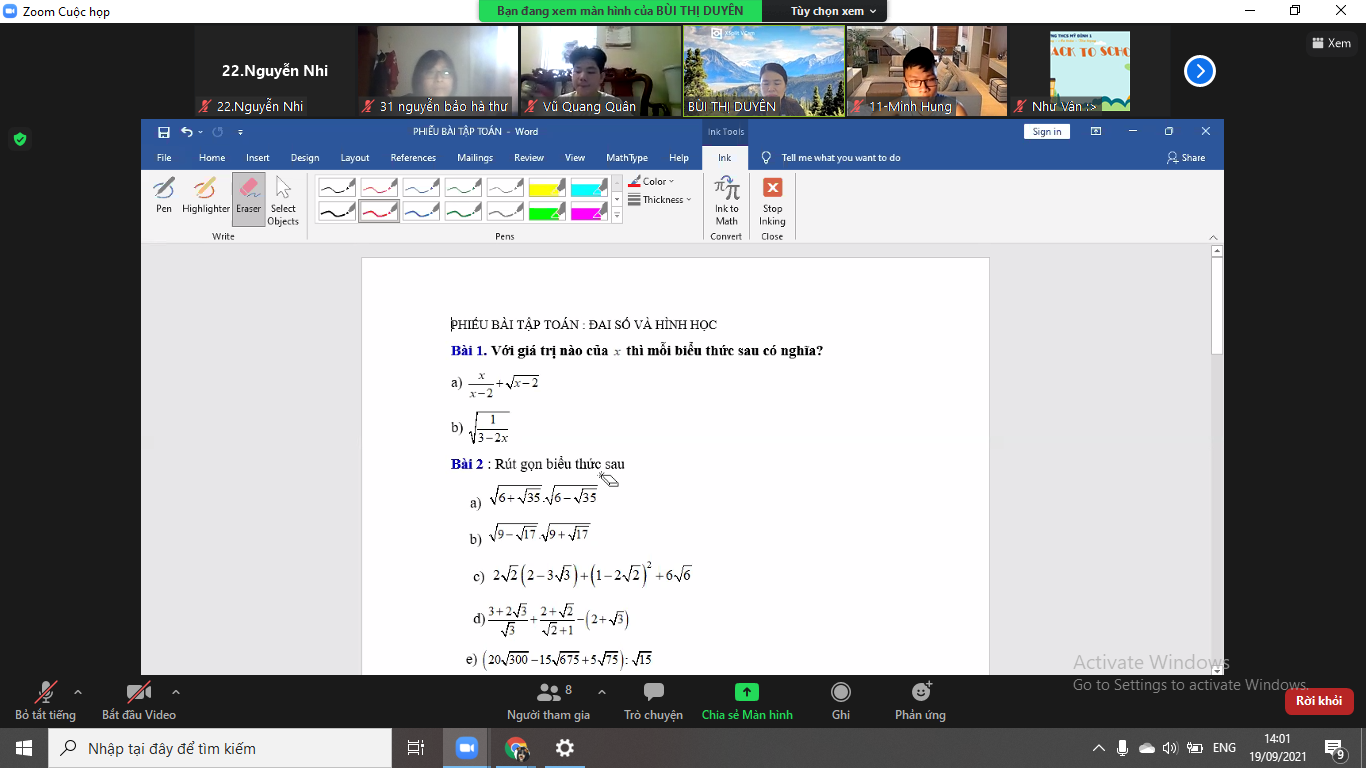
lm hộ em bài 1,2 vs ạ!!em cảm ơn
\(1,\\ a,ĐK:\left\{{}\begin{matrix}x-2\ne0\\x-2\ge0\end{matrix}\right.\Leftrightarrow x>2\\ b,ĐK:\dfrac{1}{3-2x}\ge0\Leftrightarrow3-2x\ge0\left(1>0\right)\Leftrightarrow x\le\dfrac{3}{2}\)
\(2,\\ a,=\sqrt{\left(6-\sqrt{35}\right)\left(6+\sqrt{35}\right)}=\sqrt{36-35}=\sqrt{1}=1\\ b,=\sqrt{\left(9-\sqrt{17}\right)\left(9+\sqrt{17}\right)}=\sqrt{81-17}=\sqrt{64}=8\\ c,=4\sqrt{2}-6\sqrt{6}+9-4\sqrt{2}+6\sqrt{6}=9\\ d,=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-2-\sqrt{3}=\sqrt{3}+\sqrt{2}-2-\sqrt{3}=\sqrt{2}-2\\ e,=\left(200\sqrt{3}-225\sqrt{3}+25\sqrt{3}\right):\sqrt{15}=0:\sqrt{15}=0\)
Giai hộ em ý c thôi ạ em cảm ơn
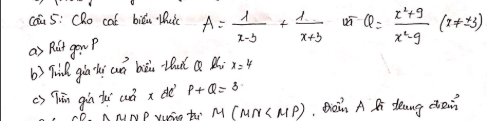
\(a,P=\dfrac{x+3+x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x}{\left(x-3\right)\left(x+3\right)}\\ b,Q=\dfrac{16+9}{16-9}=\dfrac{25}{7}\\ c,P+Q=\dfrac{2x}{\left(x-3\right)\left(x+3\right)}+\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\\ =\dfrac{2x+x^2+9}{x^2-9}=3\\ \Leftrightarrow3x^2-28=x^2+2x+9\\ \Leftrightarrow2x^2-2x-37=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+5\sqrt{3}}{2}\\x=\dfrac{1-5\sqrt{3}}{2}\end{matrix}\right.\)