Cho tam giác ABC.Vẽ ở ngoài tam giác có hình vuông ABDE và ACFH
a) CM EC=BH
b) FC vuông góc với BH
c) Gọi M,N theo thứ tự là tâm các hình vuông ABDE và ACFH.Gọi I là trung điểm BC.CM tam giác MIN là hình vuông cân
Cho tam giác ABC.Vẽ ở ngoài tam giác các hình vuông ABDE,ACFH.
a)CMR EC=BH,EC vuông góc với BH
b)Gọi M,N theo thứ tự là tâm của các hình vuông ABDE,ACFH.Gọi I là trung điểm của BC.Tam giác MIN là tam giác gì?Vì sao?
"Ai làm được mình tick cho"
Cho Tam giác ABC, ở ngoài tam giác vẽ hình vuông ABDE,ACFH
a) CMR: EC=BH, EC vuông góc với BH
b) Gọi M,N theo thứ thự là tâm các hình vuông ABDE,ACFH. Gọi I là trung điiểm BC. Tam giác MIN là hình gì? Vì sao?
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH. Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì? Vì sao?
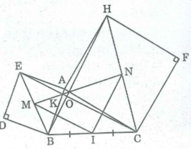
* Trong ∆ EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong ∆ BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của ∆ BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay ∠ (MIN) = 90 0
Vậy ∆ MIN vuông cân tại I.
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH
a) Chứng minh rằng \(EC=BH,EC\perp BH\)
b) Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì ? Vì sao ?
Cho tam giác nhọn ABCD. Vẽ ra phía ngoài của tam giác 2 hình vuông ABDE và ACFH.Gọi I và K lần lượt là tâm của 2 hình vuông nói trên.
a) Chứng minh EC=BH và EC vuông góc với BH
b) Gọi N là trung điểm của EH, M là trung điểm của BC.Tứ giác MINK là hình gì? Vì sao?
Đề bị sai từ câu đầu tiên. Tam giác chỉ có thể kí hiệu bằng 3 chữ cái in hoa.
Cho tam giác ABC vẽ ở phía ngoài của tam giác dựng các hình vuông ABDE và ACDF .
a ) CMR : EC = BH và EC vuông góc với BH .
b ) Gọi O1 và O2 theo thự tự lần lượt là giao điểm của các đường chéo của các hình vuông ACFH và ABDE . Gọi I là trung điểm của BC . Tam giác O1IO2 là tam giác gì ?
a. Ta thấy \(\widehat{EAC}=\widehat{BAH}\left(=\widehat{BAC}+90^o\right)\)
Vậy nên \(\Delta EAC=\Delta BAH\left(c-g-c\right)\)
Từ đó suy ra \(\widehat{ACE}=\widehat{AHB}\)
Vì \(\widehat{AHB}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{ACE}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{HJC}=90^o\)
Vậy \(EC\perp BH.\)
b. Ta thấy \(O_1\) là trung điểm EB. Vậy thì O1I là đường trung bình của tam giác BEC hay O1I // EC. Tương tự O2I // BH.
Lại có \(EC\perp BH\) nên \(O_1I\perp O_2I.\)
Vậy tam giác O1O2I là tam giác vuông tại I.
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.
a) CMR: EC = BH
b) Gọi M, N thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MNI là tamgiacs gì? Vì sao?
( Vẽ hình luôn hộ mk nha )
Cho tam giác ABC, phía ngoài tam giác ta dựng các hình vuông ABDE và ACFG.
a) Chứng minh BG=CEvà BG⊥CE .
b) Gọi M, P theo thứ tự là các trung điểm của các đoạn thẳng BC, EG và Q, N theo thứ tự là tâm của các hình vuông ABDE, ACFG. Chứng minh tứ giác MNPQ là hình vuông.
Cho tam giác ABC, phía ngoài tam giác ta dựng các hình vuông ABDE và ACFG.
a) Chứng minh BG CE = và BG⊥CE .
b) Gọi M, P theo thứ tự là các trung điểm của các đoạn thẳng BC, EG và Q, N theo thứ tự là tâm của các hình vuông ABDE, ACFG. Chứng minh tứ giác MNPQ là hình vuông.