Làm thế nào để đo chu vi của đường tròn bằng một thước kẻ và một sơi dây

Những câu hỏi liên quan
Có một sợi dây dài 4 phần 5 mét, làm thế nào để cắt ra 0,6 mét mà ko cần dùng thước để đo ?
\(\frac{4}{5}\) m = 0,8m
Đầu tiên ta gập sợi dây thành 2 đoạn thì mỗi bên sẽ là 0,4m. Sau đó ta gập đôi 1 đoạn 0,4m bất kì sẽ có 2 đoạn dài 0,2m. Kế tiếp ta sẽ giữ 1 đoạn 0,2m ở bên ngoài và duỗi thẳng đoạn 0,4m với đoạn 0,2m ở bên trong rồi cắt đoạn 0,2m bên ngoài ta được một doạn thẳng dài 0,6m được cắt từ sợi dây dài \(\frac{4}{5}\)
Đúng 0
Bình luận (0)
ko biết
Mà đây là cậu hỏi ng\\gì thế
Chả hiểu nhưng KB nhé
Đúng 0
Bình luận (0)
Đổi: \(\frac{4}{5}\)m = 0,8 m;
Đầu tiên, ta gập đôi sợi dây và cắt đôi sợi dây ra, lúc đó ta cắt được: 0.8:2=0.4 (m)
Còn lại : 0.8-0.4=0.4 (m)
Ta tiếp tục gập đôi sợi dây còn lại, cắt đôi ra. Lúc đó ta cắt được: 0.4:2=0.2 (m)
Vậy tổng cộng hai lần cắt được: 0.4+0.2=0.6(m)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Nếu dùng một sợi dây để "chia" một thanh gỗ thẳng thành hai phần dài bằng nhau thì làm thế nào ?
Lúc đầu, ta lấy 1 sợi dây, bằng thanh gỗ cần cắt. Gấp đôi sợi dây lại sao cho 2 đầu bằng nhau. Xong, ta đặt sợi dây lên thanh gỗ, sao cho 1 đầu trùng với đầu bên kia của thanh gỗ. Thế là ta đo được rồi.
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB và một điểm C trên đường tròn. Từ O kẻ một đường thẳng song song với dây AC , đường thẳng này ćt tiếp tuyến tại B của đường tròn tại điểm D.
a) Chứng minh OD là phân giác của góc BOC
b) Chứng minh CD là tiếp tuyến của đường tròn
Bán kính của hình tròn bằng trung bình cộng của số chẵn lớn nhất có một chữ số và 14 (đơn vị : cm) .Hỏi
a.Tìm đường kính của hình tròn
b.Tính chu vi hình tròn
Cho (O, R), từ một điểm M ở ngoài đường tròn (O) sao cho OM = 2R ta vẽ hai tiếp tuyến MA, MB. Một cát tuyến bất kỳ M cắt đường tròn tại C và D. Kẻ phân giác của góc CAD cắt dây CD tại E và đường tròn tại N
Ở
30
o
C
, một quả cầu thép có đường kính 6 cm và không lọt qua một lỗ tròn khoét trên một tấm đồng thau vì đường kính của lỗ nhỏ hơn 0,01 mm. Cho hệ số nở dài của thép và đồng thau lần lượt là
12
.
10
-
6
K
-
1
và
19
....
Đọc tiếp
Ở 30 o C , một quả cầu thép có đường kính 6 cm và không lọt qua một lỗ tròn khoét trên một tấm đồng thau vì đường kính của lỗ nhỏ hơn 0,01 mm. Cho hệ số nở dài của thép và đồng thau lần lượt là 12 . 10 - 6 K - 1 và 19 . 10 - 6 K - 1 . Để quả cầu lọt qua lỗ tròn cần đưa quả cầu và tấm đồng thau tới cùng nhiệt độ bằng
A. 54 , 8 o C
B. 58 , 3 o C
C. 53 , 8 o C
D. 58 , 4 o C
Chọn C
Đườngk ính quả cầu ở t o C : r = r o 1 + a 1 t - t o
Đường kính lỗ tròn ở t o C : r ' = r 0 + ∆ r 1 + a 2 t - t 0
Để quả cầu lọt qua lỗ thì r = r’.
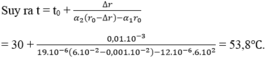
Đúng 0
Bình luận (0)
Văn bản: Phân tích tác phẩm Thế nào là sống trọn vẹn? (Theo Lâm Hoàng Phúc)
Mỗi luận điểm, lí lẽ và bằng chứng có sự kết hợp với nhau như thế nào? Phân tích một ví dụ để làm rõ.
- Mỗi luận điểm, lí lẽ và bằng chứng có sự kết hợp chặt chẽ, khăng khít với nhau; lí lẽ và bằng chứng xác thực, đáng tin cậy đưa ra để làm sáng tỏ luận điểm.
- Để lí giải cho luận điểm 2 tác giả đưa ra lí lẽ: Nếu những nỗ lực của chúng ta nhiều khi không thành công suốt đời cũng không làm được điều gì quá lớn để gửi lại thì chúng ta cũng không nên nản chí mà tiếp tục cống hiến và tạo ra thành tựu.
+ Tác giả lấy dẫn chứng: mỗi một viên gạch không tạo nên điều gì cả, nhưng khi chúng chồng lên nhau chúng tạo thành bức tường … vững chắc có thể che sóng, ngăn chiều…
Đúng 0
Bình luận (0)
Một vật chuyển động tròn đều xung quang điểm O đường kính 60 cm được gắn một thiết bị thu âm. Hình chiếu của vật này lên trục Ox đi qua tâm của đường tròn chuyển động với phương trình A Acos(10t + φ) .Một nguồn phát âm đằng hướng đặt tại điểm M trên trục Ox và cách O một khoảng 120 cm. Tại thời điểm t 0, mức cường độ âm đo được có giá trị nhỏ nhất và bằng 50 dB. Tại thời điểm mà hình chiếu của vật đạt tốc độ
1
,...
Đọc tiếp
Một vật chuyển động tròn đều xung quang điểm O đường kính 60 cm được gắn một thiết bị thu âm. Hình chiếu của vật này lên trục Ox đi qua tâm của đường tròn chuyển động với phương trình A = Acos(10t + φ) .Một nguồn phát âm đằng hướng đặt tại điểm M trên trục Ox và cách O một khoảng 120 cm. Tại thời điểm t = 0, mức cường độ âm đo được có giá trị nhỏ nhất và bằng 50 dB. Tại thời điểm mà hình chiếu của vật đạt tốc độ 1 , 5 3 m / s lần thứ 2018 thì mức cường độ âm đo được có giá trị gần với giá trị nào sau đây
A. 51 dB
B. 53 Db
C. 55 dB
D. 58dB
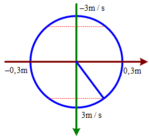
Hình chiếu của vật dao động điều hòa biên độ 30cm và tần số góc 10 rad/s
Mức cường độ âm nhỏ nhất đo được khi vật dao động tới biên âm, khi đó R = 150cm = 1,5m và L1 = 50dB
Thời điểm ban đầu vật ở biên âm, vây thời điểm vật có tốc độ 1 , 5 3 m/s lần thứ 2018 vật ở vị trí ứng với góc -π/3
Li độ của vật khi đó là x = 0,15m
Khoảng cách của vật đến nguồn là: R2 = 1,05m có mức cường độ âm L2
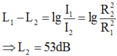
Chọn đáp án B
Đúng 0
Bình luận (0)
Cho đường tròn (O;R), một dây AB (AB < 2R) có trung điểm là H. Trên tia đối của tia BA lấy 1 điểm M và qua M kẻ các tiếp tuyến MC, MD với đường tròn (C và D là các tiếp điểm). Đường thẳng CD cắt các đường thẳng MO; OH lần lượt tại E và F.
a) CM góc CMD bằng 60 độ.
b) chứng minh OE.OM = R^2 và OH.OF = OE.OM


















