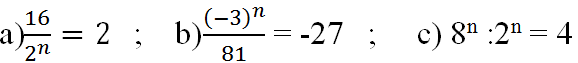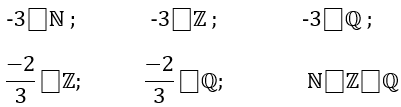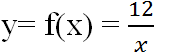bài 42 sgk toán 7 trang 23 tập 1

Những câu hỏi liên quan
Bài 42 (trang 23 SGK Toán 7 Tập 1): Tìm số tự nhiên n, biết :
GIÚP MIK VS NHA !
a) 2n = 16/2=8= 23 => n =3
b) (-3)n = (-27).81 =(-3)3.34= (-3)7 => n = 7
c) 4 =22= 23n.2n = 23n-n = 22n => n =1
Đúng 0
Bình luận (1)
Bài 1 (trang 7 SGK Toán 7 Tập 1): Điền kí hiệu (∈, ∉, ⊂) thích hợp vào ô vuông
bài tập 42 sgk lớp 7 tập 1 trang 23
a) \(\dfrac{16}{2^n}=2\Rightarrow2^n=\dfrac{16}{2}\Rightarrow2^n=8\)
Ta có: \(2^3=8\Rightarrow n=3\)
b) \(\dfrac{\left(-3\right)^n}{81}=-27\Rightarrow\left(-3\right)^n=\left(-27\right).81\)
\(\Rightarrow\left(-3\right)^n=-2187\)
Ta có: - 2187 = ( -3 ) 7
\(\Rightarrow n=7\)
c) \(8^n:2^n=4=\left(\dfrac{8}{2}\right)^n=4\Rightarrow4^n=4\)
\(\Rightarrow n=1\)
Đúng 0
Bình luận (0)
Bài 43 nữa nha mấy bạn SGK toán 6 tập 1 trang 23
Vận dụng điều lưu ý trong phần tóm tắt kiến thức.
Theo hình vẽ: Khối lượng quả bí + 100g = 1500g. Do đó khối lượng của quả bí là 1500g – 100g = 1400g.
Đúng 0
Bình luận (0)
bài 59 60 sgk toán lớp 7 trang 132 133 tập 1
?1 sgk trang 135
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
59)
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
Đúng 3
Bình luận (2)
Xem thêm câu trả lời
Giả sử 
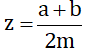
Xem thêm câu trả lời
Giả sử 
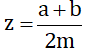
Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)
Đúng 0
Bình luận (0)
Cho hàm số
a) f(5) = ? ; f(-3) = ?
b) Hãy điền các giá trị tương ứng của hàm số vào bảng sau:
Bài 6. (Trang 23 SGK Toán 7 tập 1) Biết rằng 1 2 + 2 2 + 3 2 +…+ 102 = 385, đố em tính nhanh được tổng S = 2 2 + 4 2 + 6 2 + … + 202
Đạt A=2^2+4^2+6^2+...+20^2
A=2^2X(1^2+2^2+3^2+...+10^2) (1)
Mà 1^2+2^2+3^2+...+10^2=385(2)
Thay (2) vào (1), có: A=2^2x385
A=4X385=1540
Vậy 2^2+4^2+6^2+...+20^2 = 1540
Đúng 0
Bình luận (0)
A=2^2X(1^2+2^2+3^2+...+10^2) (1)
Mà 1^2+2^2+3^2+...+10^2=385(2)
Thay (2) vào (1), có: A=2^2x385
A=4X385=1540
Vậy 2^2+4^2+6^2+...+20^2 = 1540
Đúng 0
Bình luận (0)