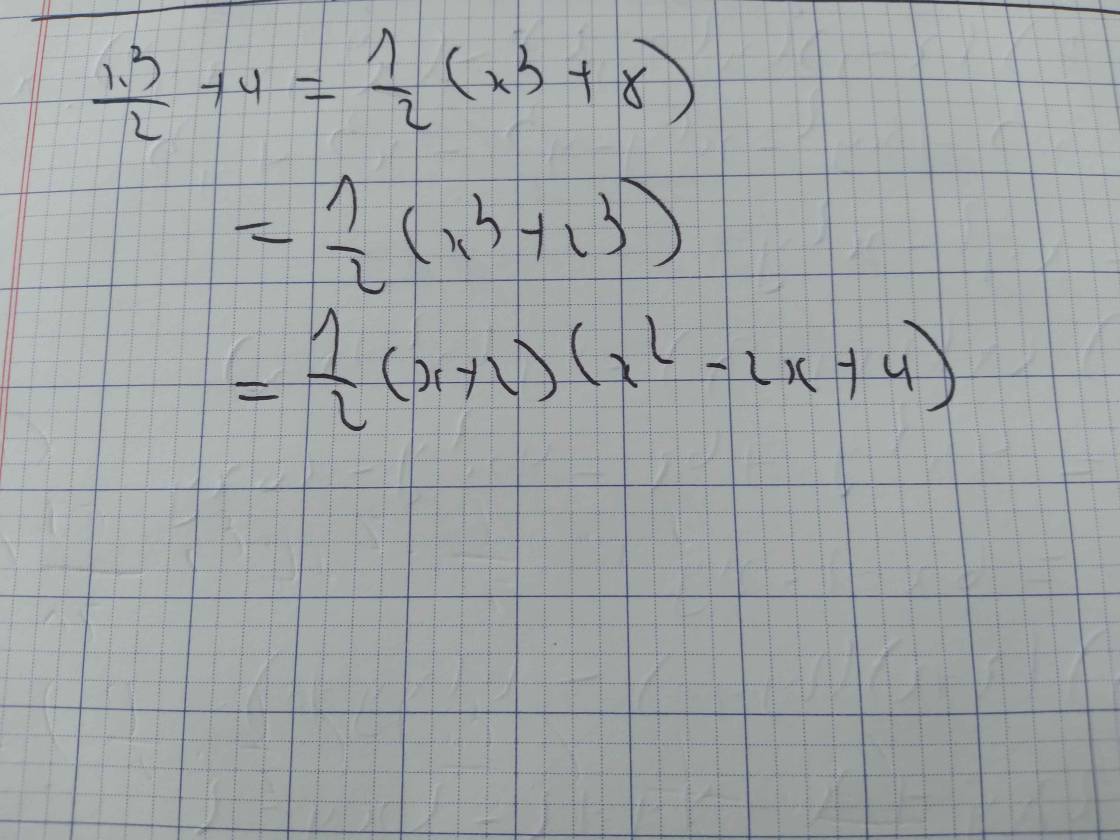Những câu hỏi liên quan
phân tích đa thức thành nhân tử (thêm bớt cùng một hạng tử):
x^3 - 2x - 4
phân tích đa thức thành nhân tử (đặt biến phụ):
x^4 + 2x^3 + 5x^2 + 4x - 12
#)Giải :
\(x^3-2x-4\)
\(=x^3+2x^2-2x^2+2x-4x-4\)
\(=x^3+2x^2+2x-2x^2-4x-4\)
\(=x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
\(x^4+2x^3+5x^2+4x-12\)
\(=x^4+x^3+6x^2+x^3+x^2+6x-2x^2-2x-12\)
\(=x^2\left(x^2+x+6\right)+x\left(x^2+x+6\right)-2\left(x^2+x+6\right)\)
\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)
\(=\left(x^2+x+6\right)\left(x-1\right)\left(x+2\right)\)
Đúng 1
Bình luận (0)
Câu 1.
Đoán được nghiệm là 2.Ta giải như sau:
\(x^3-2x-4\)
\(=x^3-2x^2+2x^2-4x+2x-4\)
\(=x^2\left(x-2\right)+2x\left(x-2\right)+2\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
Đúng 0
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử a)4(2-x)^2+xy-2y b)3a^2x-3a^2y+abx-abyBài 2: Phân tích đa thức thành nhân tử a)x(x-y)^3-y(y-x)^2-y^2(x-y) b)2ax^3+6ax^2+6ax+18aBài 3: Phân tích đa thức thành nhân tử a)x^2y-xy^2-3x+3y b)3ax^2+3bx^2+bx+5a+5bBài 4: Tính giá trị biểu thức Aa(b+3)-b(3+b) tại a2003 và b1997Bài 5: Tìm x, biếta)8x(x-2017)-2x+40340 b)x^2(x-1)+16(1-x)0
Đọc tiếp
Bài 1: Phân tích đa thức thành nhân tử
a)4(2-x)\(^2\)+xy-2y b)3a\(^2\)x-3a\(^2\)y+abx-aby
Bài 2: Phân tích đa thức thành nhân tử
a)x(x-y)\(^3\)-y(y-x)\(^2\)-y\(^2\)(x-y) b)2ax\(^3\)+6ax\(^2\)+6ax+18a
Bài 3: Phân tích đa thức thành nhân tử
a)x\(^2\)y-xy\(^2\)-3x+3y b)3ax\(^2\)+3bx\(^2\)+bx+5a+5b
Bài 4: Tính giá trị biểu thức
A=a(b+3)-b(3+b) tại a=2003 và b=1997
Bài 5: Tìm x, biết
a)8x(x-2017)-2x+4034=0 b)x\(^2\)(x-1)+16(1-x)=0
\(1,\\ a,=4\left(x-2\right)^2+y\left(x-2\right)=\left(4x-8+y\right)\left(x-2\right)\\ b,=3a^2\left(x-y\right)+ab\left(x-y\right)=a\left(3a+b\right)\left(x-y\right)\\ 2,\\ a,=\left(x-y\right)\left[x\left(x-y\right)^2-y-y^2\right]\\ =\left(x-y\right)\left(x^3-2x^2y+xy^2-y-y^2\right)\\ b,=2ax^2\left(x+3\right)+6a\left(x+3\right)\\ =2a\left(x^2+3\right)\left(x+3\right)\\ 3,\\ a,=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\\ b,Sửa:3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\\ 4,\\ A=\left(b+3\right)\left(a-b\right)\\ A=\left(1997+3\right)\left(2003-1997\right)=2000\cdot6=12000\\ 5,\\ a,\Leftrightarrow\left(x-2017\right)\left(8x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Phân tích đa thức thành nhân tử:
$x^4+4$
\(x^4+4=x^4+4+4x^2-4x^2\)
\(=\left(x^4+4x^2+4\right)-\left(2x\right)^2\)
\(=\left(x^2+2\right)^2-\left(2x\right)^2=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
Đúng 0
Bình luận (0)
\(x^4+4=\left(x^4+4x^2+4\right)-4x^2=\left(x^2+2\right)^2-\left(2x\right)^2=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
Đúng 0
Bình luận (0)
Đa thức x^3 - 2x^2 + x - xy^2 được phân tích thành nhân tử
Đa thức x^3 + 3x^2y +3xy^2 + y^3 được phân tích thành nhân tử là
Đa thức 4x(2y-z)+7y(2y-z) được phân tích thành nhân tử là:
Đa thức x^2+4x+4 được phân tích thành nhân tử là
Tìm x biết x(x-2)-x+2
\(1,=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-y-1\right)\left(x+y-1\right)\\ 2,=\left(x+y\right)^3\\ 3,=\left(2y-z\right)\left(4x+7y\right)\\ 4,=\left(x+2\right)^2\\ 5,Sửa:x\left(x-2\right)-x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
X^4+4y^4 phân tích đa thức thành nhân tử
x4 + 4y4
= (x2)2 + 4x2y2 + (2y2)2 - 4x2y2
= (x2 + 2y2)2 - (2xy)2
= (x2 + 2y2 - 2xy)(x2 + 2y2 + 2xy)
Đúng 0
Bình luận (0)
\(x^4+4y^4\)
\(=\left(x^2\right)^2+\left(2y\right)^2+4x^2y^2-4x^2y^2\)
\(=\left(x^2\right)^2+4x^2y^2+\left(2y\right)^2-4x^2y^2\)
\(=\left[\left(x^2\right)^2+4x^2y^2+\left(2y\right)^2\right]-\left(2xy\right)^2\)
\(=\left(x^2+2y^2\right)^2-\left(2xy\right)^2\)
\(=\left(x^2+2y^2-2xy\right)\left(x^2+2y^2+2xy\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử x^4+y^4
\(x^4+y^4\)
\(=x^4+2x^2y^2+y^4-2x^2y^2\)
\(=\left(x^2+y^2\right)^2-\left(\sqrt{2}xy\right)^2\)
\(=\left(x^2+\sqrt{2}xy+y^2\right)\left(x^2-\sqrt{2}xy+y^2\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử x³/2+4
phân tích đa thức thành nhân tử bằng phương pháp thêm bớt hạng tử để xuất hiện hằng đăng thức
x^4 + x^2 +1
phân tích đa thức thành nhân tử bằng phương pháp thêm hạng tử để xuất hiện thừa số chung
x^5 - x^4 - 1
x - x^10 + x^5 + 1
x^4+x^2+1 = (x^4+2x^2+1)-x^2 = (x^2+1)^2-x^2 = (x^2-x+1).(x^2+x+1)
k mk nha
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử bằng phương pháp thêm bớt hạng tử để xuất hiện hằng đăng thức
x^4 + x^2 +1
phân tích đa thức thành nhân tử bằng phương pháp thêm hạng tử để xuất hiện thừa số chung
x^5 - x^4 - 1
x - x^10 + x^5 + 1
x5-x4-1=x5-x3-x2-x4+x2+x+x3-x-1
=x2.(x3-x-1)-x.(x3-x-1)+(x3-x-1)
=(x3-x-1)(x2-x+1)
Đúng 0
Bình luận (0)
x^4+x^2+1 = (x^4+2x^2+1)-x^2 = (x^2+1)^2-x^2 = (x^2-x+1).(x^2+x+1)
k mk nha
Đúng 0
Bình luận (0)
phân tích đa thức sau thành nhân tử 1 x^2 (4-x) + 9 (4-x)
\(x^2\left(4-x\right)+9\left(4-x\right)=\left(x^2+9\right)\left(4-x\right)\)
Đúng 2
Bình luận (0)