cho ▲ABC nhọn. CM: 4.SABC.(cotA+cotB+cotC)=AB2+AC2+BC2

Những câu hỏi liên quan
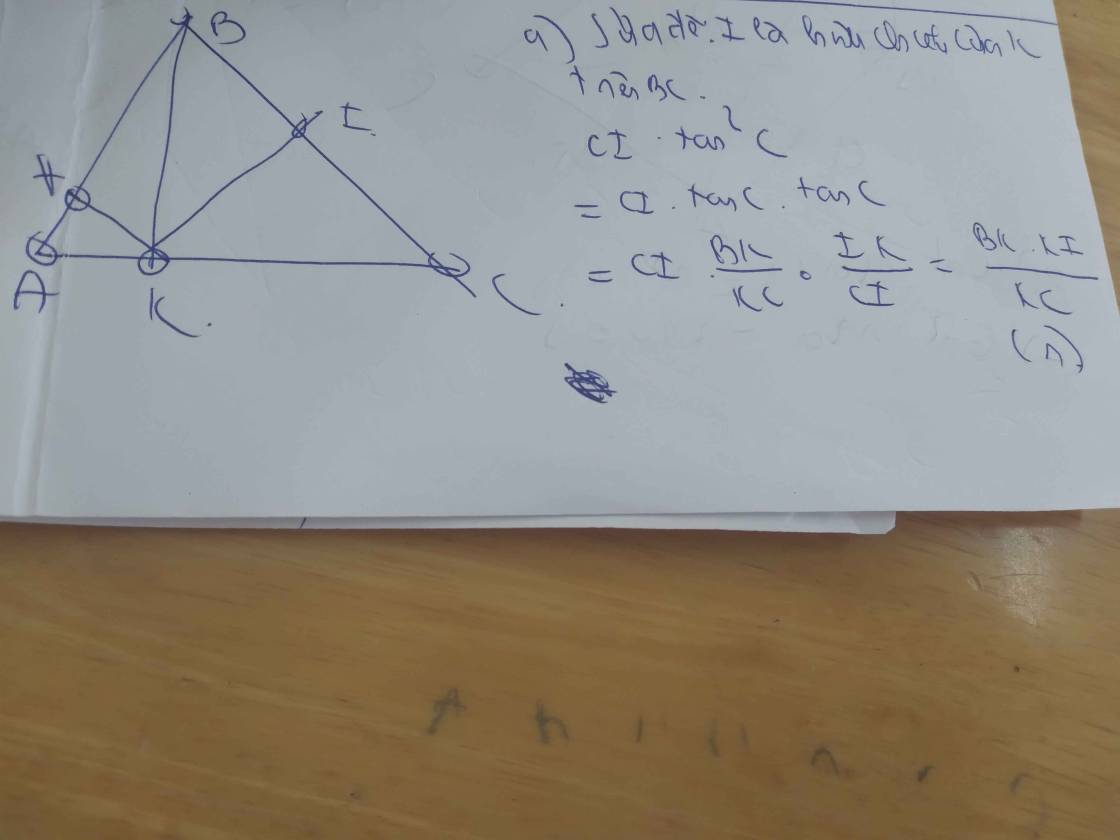
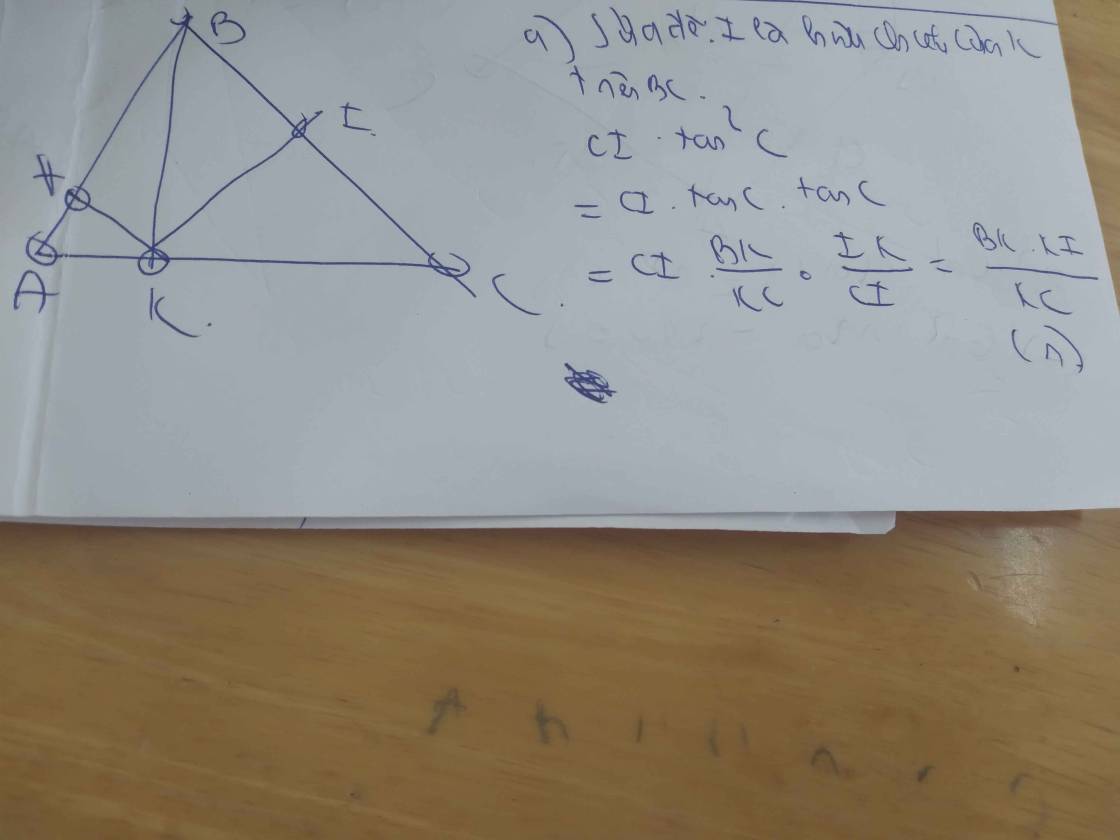
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
a) BI=CI.tan2CC
b) SABC=AC2/2(cotA+cotC)
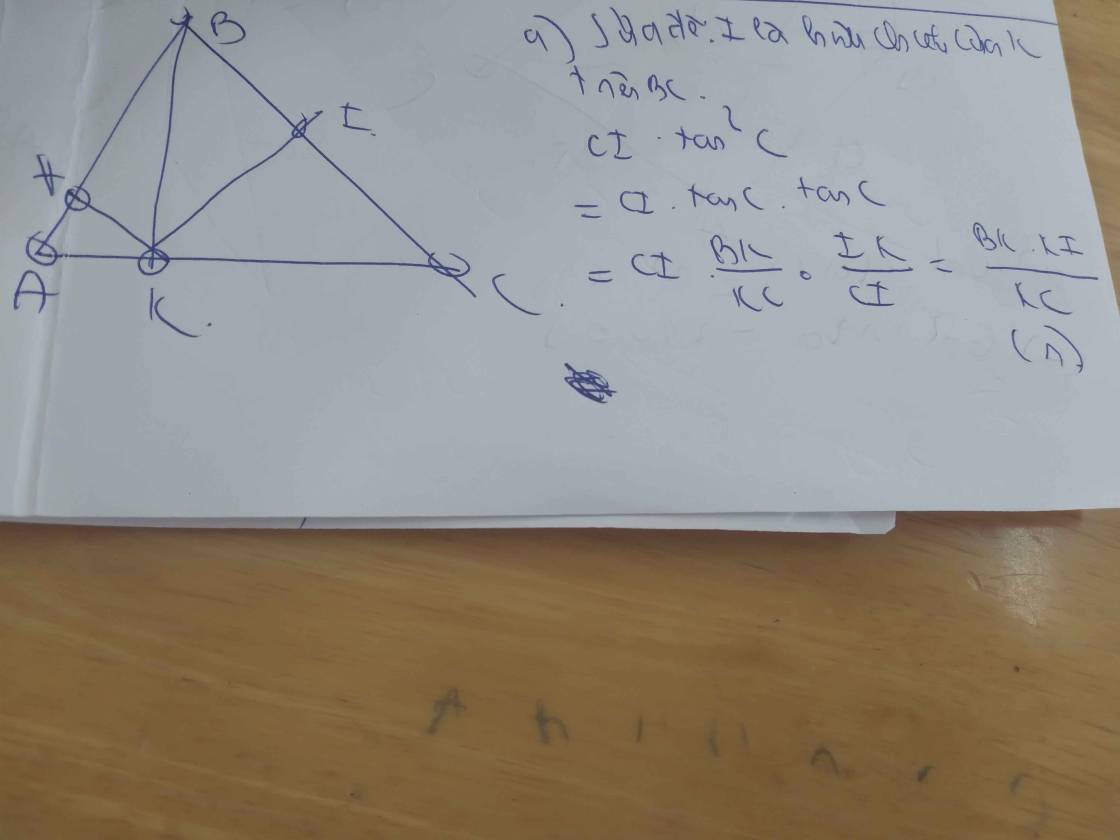
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
a) BI=CI.tan2CC
b) SABC=AC2/2(cotA+cotC)
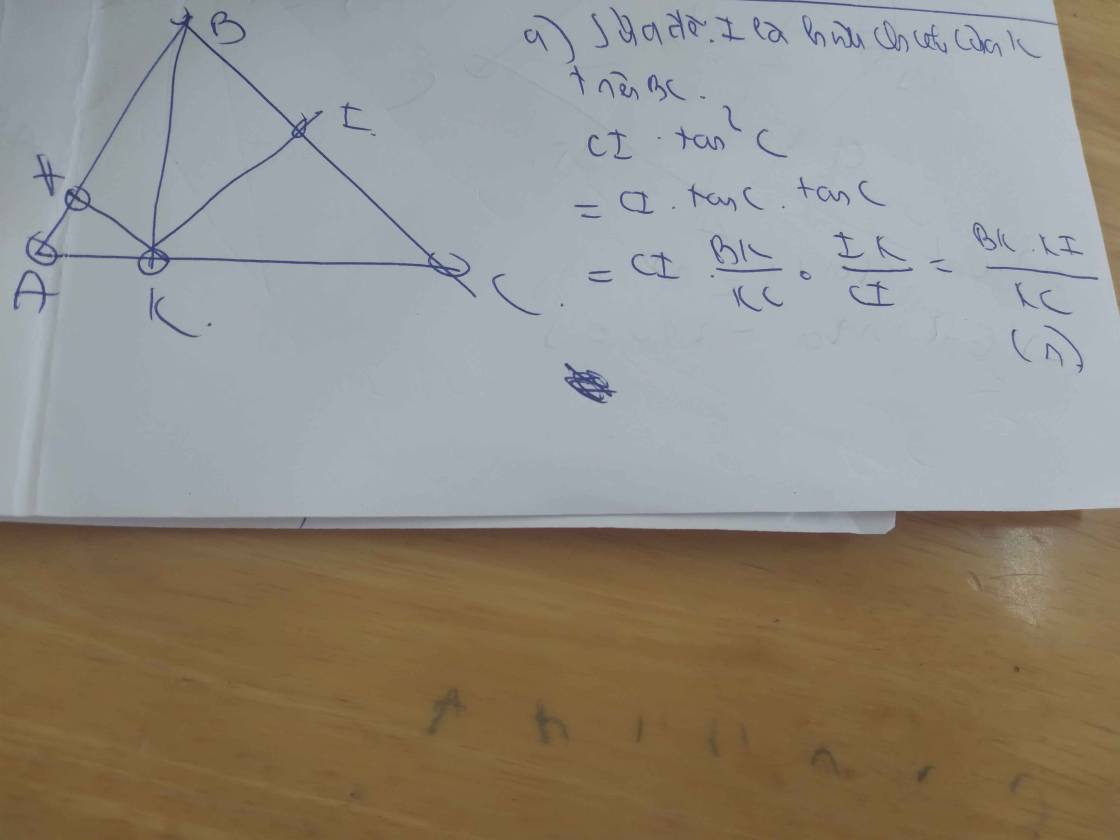
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
2CC
ABC=AC2/2(cotA+cotC)
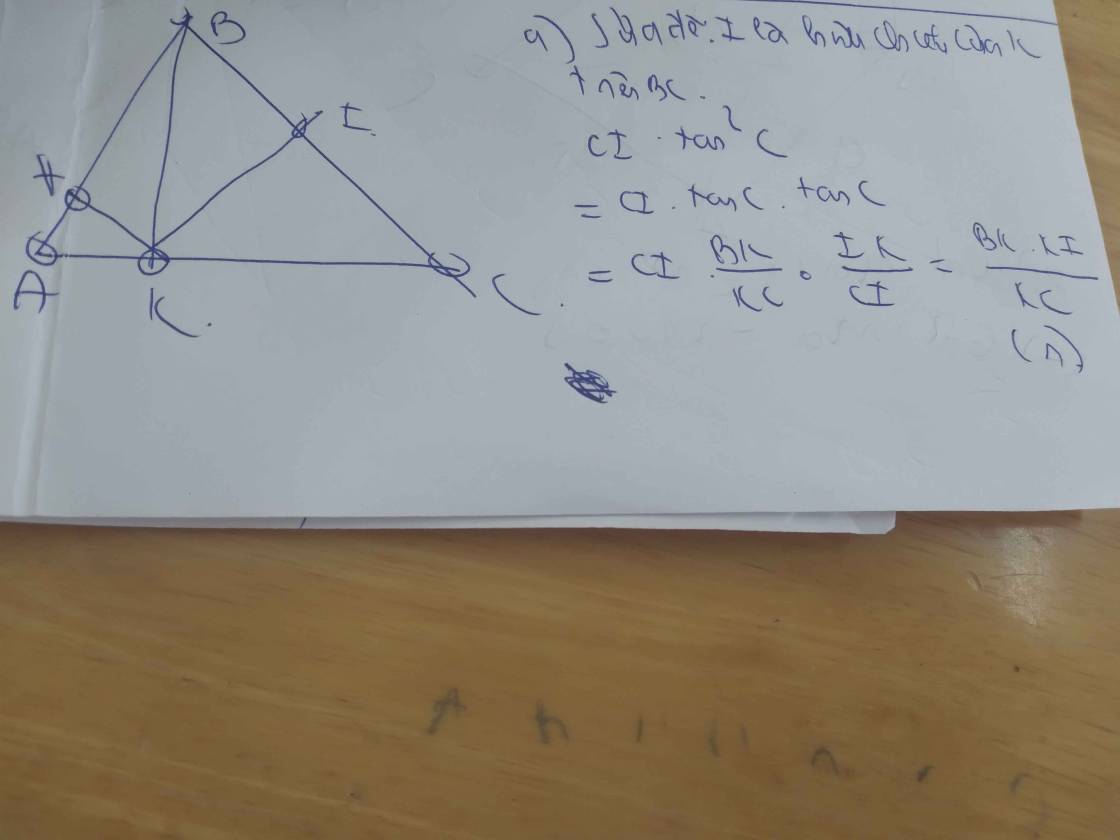
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
a) BI=CI.tan2CC
b) SABC=AC2/2(cotA+cotC)
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
a) BI=CI.tan2CC
b) SABC=AC2/2(cotA+cotC)
cho ▲ABC nhọn. CM: 4SABC.(cotA+cotB+cotC)=AB2+AC2+BC2
cho tam giác ABC nhọn. cmr cotA+cotB+cotC=AB^2+AC^2+BC^2/4S
cho tam giác ABC nhọn. chứng minh rằng cotA+cotB+cotC <= 3/2
Cho tam giác ABC nhọn không cân. M là điểm trên BC. Đặt BM/CM=m/n, góc BAM = alpha, góc AMB= beta. Chứng minh
a) (m+n)*cotB=m*cotC -n*cotB
b) m*cot alpha =(m+n)cotA+n*cotB