Các câu hỏi tương tự
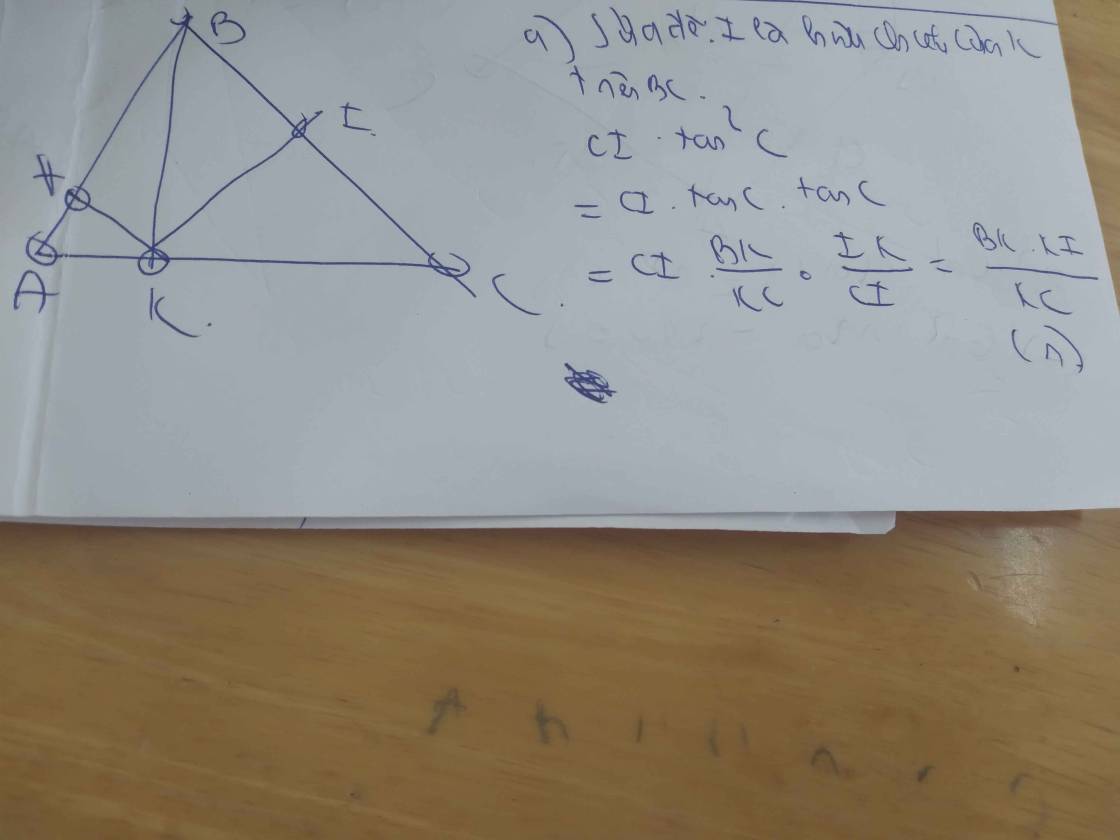
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
a) BI=CI.tan2CC
b) SABC=AC2/2(cotA+cotC)
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
a) BI=CI.tan2CC
b) SABC=AC2/2(cotA+cotC)
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
2CC
ABC=AC2/2(cotA+cotC)
△ABC nhọn (AB<AC) đường cao BK. Gọi H,I lần lượt là hình chiếu của K trên AB, AC. Chứng minh rằng
a) BI=CI.tan2CC
b) SABC=AC2/2(cotA+cotC)
Cho tam giác ABC và đường cao AH. Gọi I, K lần lượt là hình chiếu của H trên AB, AC
Cho tam giác ABC và đường cao AH. Gọi I, K lần lượt là hình chiếu của H trên AB, AC.
a) Chứng minh ED // IK
Xem chi tiết
a) Chứng minh ED // IK
Cho tam giác ABC nhọn (AB<AC). Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. Gọi H là giao điểm của BE và CF
a) Đường cao FQ của tam giác BFC cắt BE ở I chứng minh AB là tiếp tuyếncủa đường tròn (EFI)
b) Gọi K là hình chiếu của E trên BC. chứng minh BK<CQ
cho tam giác ABC nhọn, đường cao AH. Lấy D, E lần lượt là hình chiếu của H trên AB, AC. Gọi F là hình chiếu của A trên DE, K là hình chiếu của H trên DE. Chứng minh DE=EF
Cho tam giác ABC vuông tại A có AB 30cm, AC 40cm.a) Giải tam giác ABC.b) Kẻ đường cao AH. Tính AH, BH.c) Gọi I, K lần lượt là hình chiếu của H lên AB và AC. Chứng minh: 1/ IK2 1/ AB2 + 1/ AC2 . (dấu / nghĩa là phần, thay cho phân số) ; (số 2 kế bên chữ là mủ 2 [bình phương])
Đọc tiếp
Cho tam giác ABC vuông tại A có AB= 30cm, AC= 40cm.
a) Giải tam giác ABC.
b) Kẻ đường cao AH. Tính AH, BH.
c) Gọi I, K lần lượt là hình chiếu của H lên AB và AC. Chứng minh:
1/ IK2 = 1/ AB2 + 1/ AC2 . (dấu " / " nghĩa là phần, thay cho phân số) ; (số 2 kế bên chữ là mủ 2 [bình phương])
cho tam giác ABC nhọn, đường cao AH, gọi M, N lần lượt là hình chiếu của H trên AB, AC. Chứng minh MN= AH.sinA