Bài 6: 

a: \(2^{27}=8^9\)

\(3^{18}=9^9\)

b: Vì \(8^9< 9^9\)

nên \(2^{27}< 3^{18}\)

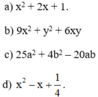
a) x2 + 2x + 1

= x2 + 2.x.1 + 12

= (x + 1)2 (Áp dụng hằng đẳng thức (1) với A = x và B = 1)

b) 9x2 + y2 + 6xy

= 9x2 + 6xy + y2

= (3x)2 + 2.3x.y + y2

= (3x + y)2 (Áp dụng hằng đẳng thức (1) với A = 3x và B = y)

c) 25a2 + 4b2 – 20ab

= 25a2 – 20ab + 4b2

= (5a)2 – 2.5a.2b + (2b)2

= (5a – 2b)2 (Áp dụng hằng đẳng thức (2) với A = 5a và B = 2b)

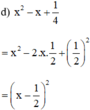
(Áp dụng hằng đẳng thức (2) với A = x và B = 1/2 )

\(\frac{9.3^3.1}{81.3^2}=\frac{3.3^3}{3^4.3^2}=\frac{3^4}{3^6}=3^{4-6}=3^{-2}\) . 3^-2 với dạng aⁿ

a: Sửa đề: 3^2

\(=3^2\cdot\dfrac{1}{3^5}\cdot3^8\cdot\dfrac{1}{3^3}=3^2\)

b: \(=3^{\left(-2\right)\cdot\left(-2\right)}\cdot\dfrac{1}{3^5}\cdot3^3=\dfrac{3^4}{3^2}=3^2\)

c: \(=2^{12}\cdot2^{16}\cdot2^4=2^{32}\)

d: \(=\left[\dfrac{1}{9}\cdot\dfrac{27}{8}\cdot3\right]\cdot\dfrac{128}{81}\)

\(=\dfrac{16}{9}=\left(\dfrac{4}{3}\right)^2\)

Bài 1: 

a) \(4^8\cdot2^{20}=\left(2^2\right)^8\cdot2^{20}=2^{36}\)

 \(64^3\cdot4^5=\left(2^6\right)^3\cdot\left(2^2\right)^5=2^{18}\cdot2^{10}=2^{28}\)

\(y\cdot y^7=y^{1+7}=y^8\)

\(a^n\cdot a^2=a^{n+2}\)

Bài 1:

b) \(10^8:2^8=5^8\)

\(17^8:17^5=17^3\)

\(2^{25}:32^4=2^{25}:2^{20}=2^5\)

\(19^4:9^4=\left(\dfrac{19}{9}\right)^4\)

Bài 2: 

a) Ta có: \(2^x\cdot4=128\)

nên \(2^x=32\)

hay x=5

b) Ta có: \(3^x=81\)

nên \(3^x=3^4\)

hay x=4