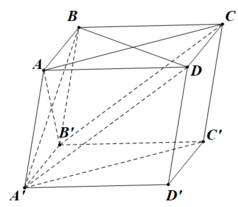
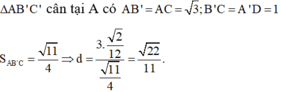cho khối hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau và bằng a ,góc A'AB=góc BAD= góc A'AD=α (00<α<900).hãy tính thể tích của khối hộp

Những câu hỏi liên quan
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh bằng nhauvaf bằng a.Biết A'AD=A'AB=BAD=60. Tính diện tích S của mặt cầu ngoại tiếp tứ diện A.A'BD.
Hình hộp ABCD.ABCD có AB AA AD a và
A
A
B
^
A
A
D
^
B
A
D
^
60
°
Khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện AABD bằng A. ...
Đọc tiếp
Hình hộp ABCD.A'B'C'D' có AB = AA' = AD = a và A ' A B ^ = A ' A D ^ = B A D ^ = 60 ° Khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện A'ABD bằng
A. a 2
B. a 2 2
C. a 3 2
D. 2a
Cho hình hộp ABCD.A'B'C'D' tất cả các cạnh đều bằng a, góc BAD = 60 độ, hình chiếu vuông góc của A' xuống (ABCD) trùng với trung điểm của AB. Tính thể tích khối hộp ABCD.A'B'C'D'.
Cho hình hộp ABCD.ABCD có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng
60
0
. Tính khoảng cách giữa hai đường thẳng AB và AC
A
.
22
11
B
.
2
11
C
.
2
11
D
.
...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 0 . Tính khoảng cách giữa hai đường thẳng AB' và A'C'
A . 22 11
B . 2 11
C . 2 11
D . 3 11
Đáp án A.
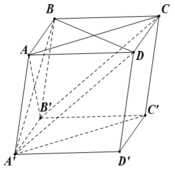
Ta có AA'BC là chóp đều có tất cả các cạnh bằng 1
![]()
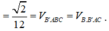
Ta có ![]()
![]()
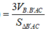
Lại có
∆
AB'C có B'C = A'D = 1; ![]() (do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
(do là hình thoi cạnh 1 có
B
A
D
^
=
60
0
)
Do đó
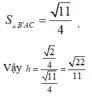
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 ° . Tính khoảng cách giữa hai đường thẳng AB' và A'C'
A. 22 11
B. 2 11
C. 2 11
D. 3 11
Cho hình hộp ABCD.ABCD có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng
60
o
. Tính khoảng cách giữa hai đường thẳng AB và A C
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 o . Tính khoảng cách giữa hai đường thẳng AB' và A' C'
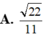
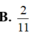
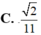
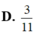
Cho hình hộp
A
B
C
D
.
A
B
C
D
có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng
60
∘
. Tính khoảng cách giữa hai đường thẳng
A
B
v
à
A
C
A.
22
11
B. ...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 ∘ . Tính khoảng cách giữa hai đường thẳng A B ' v à A ' C '
A. 22 11
B. 2 11
C. 2 11
D. 3 11
Đáp án A
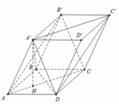
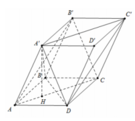
Do các góc phẳng đỉnh A đều bằng 60 ∘ và
nên các tam giác A ’ A D ; A ’ A B ; A B D là các tam giác đều cạnh 1.
Ta có:
A ' C ' / / A C ⇒ d A B ' ; A ' C ' = d A B ' C ; A ' C ' = d C ' ; A B ' C = 3 V C ' . A B ' C S . A B ' C
Mặt khác A ’ . A B D là hình tứ diện đều cạnh 1.
Ta có A H = 2 3 . A O = 3 3 ⇒ A ' H = A A ' 2 − A H 2 = 6 3 .
V = S A B C D = V A . C C ' B ' = 1 2 V A . C C ' B ' B = V 6 = 2 12
Δ A B ' C ' cân tại A có A B ' = A C = 3 ; B ' C = A ' D = 1
S A B ' C = 11 4 ⇒ d = 3. 2 12 11 4 = 22 11 .
Đúng 0
Bình luận (0)
Hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau. Chứng minh rằng AC ⊥ B'D', AB' ⊥ CD' và AD' ⊥ CB'. Khi mặt phẳng (AA'C'C) vuông góc với mặt phẳng (BB'D'D)?
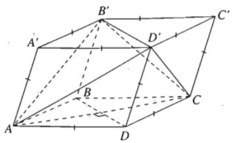
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Ta có ABCD là hình thoi nên AC ⊥ BD
Theo tính chất của hình hộp: BD // B'D', do đó AC ⊥ B'D'.
Chứng minh tương tự ta được AB' ⊥ CD', AD' ⊥ CB'
Hai mặt phẳng (AA'C'C) và (BB'D'D) vuông góc với nhau khi hình hộp ABCD.A'B'C'D'là hình lập phương.
Đúng 0
Bình luận (0)
Toán 11 : cho hình hộp abcd.a'b'c'd' có tất cả các cạnh bằng a .góc bad = 60 độ . Góc baa'=daa'=60 độ
a, Tính góc giữa ab và a'd ; ac' và b'd
b, Tính diện tích của a'b'cd và acc'a'
c, Tính góc giữa ac' với các đường thẳng ab,ad,aa'
cho hình hộp ABCD.A'B'C'D' có các cạnh đều =a. góc BAD =60•, BAB' =DAD'=120•.tính góc giữa đường thẳng AB và A'D',AC',B'D.tính diện tích A'B'CD và A'CC'A'
Đúng 0
Bình luận (0)