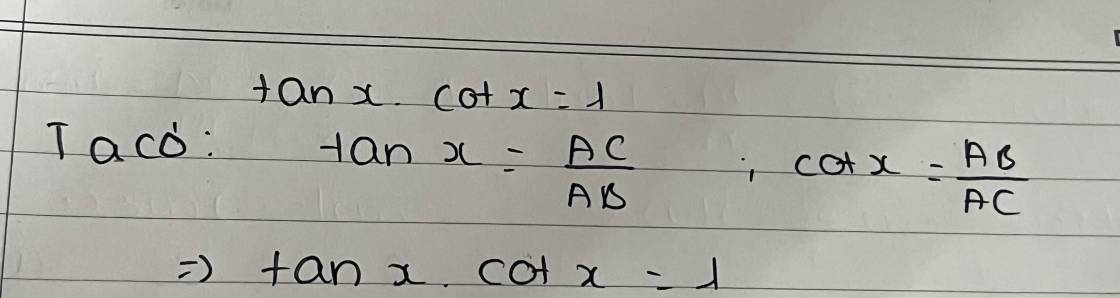Cho tam giác ABC.CMR:
tan(A/2)tan(B/2)+tan(B/2)tan(C/2)+tan(C/2)tan(A/2)=1
Những câu hỏi liên quan
Cho tam giác ABC có số đo 3 góc là A, B, C thỏa mãn điều kiện \(\tan\dfrac{A}{2}+\tan\dfrac{B}{2}+\tan\dfrac{C}{2}=\sqrt{3}\) . Tam giác ABC là tam giác gì ?
\(\dfrac{A}{2}+\dfrac{B}{2}=\dfrac{\pi}{2}-\dfrac{C}{2}\Rightarrow tan\left(\dfrac{A}{2}+\dfrac{B}{2}\right)=tan\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)\)
\(\Rightarrow\dfrac{tan\dfrac{A}{2}+tan\dfrac{B}{2}}{1-tan\dfrac{A}{2}tan\dfrac{B}{2}}=cot\dfrac{C}{2}=\dfrac{1}{tan\dfrac{C}{2}}\)
\(\Rightarrow tan\dfrac{A}{2}.tan\dfrac{C}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}=1-tan\dfrac{A}{2}tan\dfrac{B}{2}\)
\(\Rightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=1\)
Ta có:
\(tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\ge\sqrt{3\left(tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}\right)}=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(A=B=C\) hay tam giác ABC đều
Đúng 2
Bình luận (0)
cho tam giác ABC .chứng minh
\(sin\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}+sin\frac{B}{2}cos\frac{C}{2}cos\frac{A}{2}+sin\frac{C}{2}cos\frac{A}{2}cos\frac{B}{2}=sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}+tan\frac{A}{2}tan\frac{B}{2}+tan\frac{B}{2}tan\frac{C}{2}+tan\frac{C}{2}tan\frac{A}{2}\)
Tự chứng minh từng cái này rồi suy ra cái đó nhé b.
Ta có: \(sin\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}-sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}=sin^2\frac{A}{2}\)
Tương tự ta suy ra:
\(sin\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}+cos\frac{A}{2}sin\frac{B}{2}cos\frac{C}{2}+cos\frac{A}{2}cos\frac{B}{2}sin\frac{C}{2}=sin^2\frac{A}{2}+sin^2\frac{B}{2}+sin^2\frac{C}{2}+3sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}\left(1\right)\)
Tiếp theo chứng minh:
\(2sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}=\frac{cosA+cosB+cosC-1}{2}\left(2\right)\)
\(sin^2\frac{A}{2}+sin^2\frac{B}{2}+sin^2\frac{C}{2}=\frac{3}{2}-\frac{cosA+cosB+cosC}{2}\left(3\right)\)
\(tan\frac{A}{2}tan\frac{B}{2}+tan\frac{B}{2}tan\frac{C}{2}+tan\frac{C}{2}tan\frac{A}{2}=1\left(4\right)\)
Từ (1), (2), (3), (4) suy được điều phải chứng minh
Đúng 0
Bình luận (0)
trinh le na
cho bạn 4 năm nữa cũng chưa hiểu đâu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:1, sin A + sin B - sin C 4sindfrac{A}{2} sin dfrac{B}{2}sin dfrac{C}{2}2, dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}tandfrac{A}{2}tandfrac{B}{2}tandfrac{C}{2} (ΔABC nhọn)3, dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}tandfrac{A}{2}+tandfrac{B}{2}+tandfrac{C}{2}GIÚP MÌNH VỚI!!!
Đọc tiếp
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:
1, sin A + sin B - sin C = 4sin\(\dfrac{A}{2}\) sin \(\dfrac{B}{2}\)sin \(\dfrac{C}{2}\)
2, \(\dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}=tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\) (ΔABC nhọn)
3, \(\dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}=tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\)
GIÚP MÌNH VỚI!!!
1.
\(sinA+sinB-sinC=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-sin\left(A+B\right)\)
\(=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-2sin\dfrac{A+B}{2}.cos\dfrac{A+B}{2}\)
\(=2sin\dfrac{A+B}{2}.\left(cos\dfrac{A-B}{2}-cos\dfrac{A+B}{2}\right)\)
\(=2sin\dfrac{A+B}{2}.2sin\dfrac{A}{2}.sin\dfrac{B}{2}\)
\(=4sin\dfrac{A}{2}.sin\dfrac{B}{2}.cos\dfrac{C}{2}\)
Sao t lại đc như này v, ai check hộ phát
Đúng 0
Bình luận (0)
12 tháng 4 2022 lúc 20:33
A+B+C=pi
chứng minh: tan(A/2).tan(B/2)+tan(B/2).tan(C/2)+tan(A/2).tan(C/2)=1
\(A+B+C=\pi\Rightarrow\dfrac{A}{2}+\dfrac{B}{2}=\dfrac{\pi}{2}-\dfrac{C}{2}\)
\(\Rightarrow tan\left(\dfrac{A}{2}+\dfrac{B}{2}\right)=tan\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)\)
\(\Rightarrow\dfrac{tan\dfrac{A}{2}+tan\dfrac{B}{2}}{1-tan\dfrac{A}{2}tan\dfrac{B}{2}}=cot\dfrac{C}{2}=\dfrac{1}{tan\dfrac{C}{2}}\)
\(\Rightarrow\left(tan\dfrac{A}{2}+tan\dfrac{B}{2}\right)tan\dfrac{C}{2}=1-tan\dfrac{A}{2}tan\dfrac{B}{2}\)
\(\Rightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=1\)
Đúng 1
Bình luận (0)
Bạn nào giúp mình vs nhá:thanks mọi người nhiều lắm^^
1/ cho tam giác ABC. cmr:
dfrac{1}{sinA}+dfrac{1}{sinB}+dfrac{1}{sinC}dfrac{1}{2}.left(tandfrac{A}{2}+tandfrac{B}{2}+tandfrac{C}{2}+cotdfrac{A}{2}.cotdfrac{B}{2}.cotdfrac{C}{2}right)
2,cmr:
left(a-bright)tandfrac{A}{2}.tandfrac{B}{2}+left(b-cright)tandfrac{B}{2}.tandfrac{C}{2}+left(c-aright)tandfrac{C}{2}.tandfrac{A}{2}0
Đọc tiếp
Bạn nào giúp mình vs nhá:===thanks mọi người nhiều lắm^^
1/ cho tam giác ABC. cmr:
\(\dfrac{1}{sinA}+\dfrac{1}{sinB}+\dfrac{1}{sinC}=\dfrac{1}{2}.\left(tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}+cot\dfrac{A}{2}.cot\dfrac{B}{2}.cot\dfrac{C}{2}\right)\)
2,cmr:
\(\left(a-b\right)tan\dfrac{A}{2}.tan\dfrac{B}{2}+\left(b-c\right)tan\dfrac{B}{2}.tan\dfrac{C}{2}+\left(c-a\right)tan\dfrac{C}{2}.tan\dfrac{A}{2}=0\)
cho tam giác ABC nhọn.chứng minh:
tan2A+tan2B+tan2C>4(cot2A+cot2B+cot2C)
Chứng minh trong mọi tam giác ABC ta đều có :
a) \(\tan\frac{A}{2}.\tan\frac{B}{2}+\tan\frac{B}{2}.\tan\frac{C}{2}+\tan\frac{C}{2}.\tan\frac{A}{2}=1\)
b) \(\cot A.\cot B+\cot B.\cot C+\cot C.\cot A=1\)
1. Căn bậc ba của `8` là?
2. Tính \(\sqrt{16a^2}\)
3. Trục căn thức dưới mẫu của \(\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}\) là?
4. Cho tam giác ABC vuông ở C, hệ thức nào đúng:
`a) tan B = (AB)/(BC)`
`b) tan B = (AC)/(AB)`
`c) tan B = (AC)/(BC)`
`d) tan B = (AB)/(AC)`
1. \(\sqrt[3]{8}=2.\)
2. \(A=\sqrt{16a^2}=4\left|a\right|\)
\(\Rightarrow\left[{}\begin{matrix}A=4a\left(a\ge0\right)\\A=-4a\left(a< 0\right)\end{matrix}\right..\)
3. \(B=\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}=\dfrac{\left(9-2\sqrt{3}\right)\left(3\sqrt{6}+2\sqrt{2}\right)}{\left(3\sqrt{6}\right)^2-\left(2\sqrt{2}\right)^2}=\dfrac{23\sqrt{6}}{46}=\dfrac{\sqrt{6}}{2}.\)
4. C.
Đúng 1
Bình luận (5)
Cho tam giác abc nhọn. Chứng minh: Sabc= bc^2.tan b.tan c / 2.(tan b+tan c)
giúp mình với ạ
ý của bạn là cotang đk ạ chứ mình thấy cos nó sai ý
Đúng 0
Bình luận (0)