Theo đề, ta có:\(\hept{\begin{cases}\widehat{A}=2\widehat{B}\\\widehat{C}-\widehat{B}=36^0\end{cases}\Rightarrow\hept{\begin{cases}\widehat{A}=2\widehat{B}\\\widehat{C}=36^0+\widehat{B}\end{cases}}}\)

\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (tổng ba góc của một tam giác)

\(\Rightarrow2\widehat{B}+\widehat{B}+36^0+\widehat{B}=180^0\)

\(\Rightarrow4\widehat{B}=144^0\Rightarrow\widehat{B}=36^0\)

                               \(\widehat{A}=2\widehat{B}=2.36^0=72^0\)

                                \(\widehat{C}=180^0-36^0-72^0=72^0\)

b) \(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{2}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+1+2}=\frac{180^0}{6}=30^0\)

\(\Rightarrow\hept{\begin{cases}\widehat{A}=30^0.3=90^0\\\widehat{B}=30^0.1=30^0\\\widehat{C}=30^0.2=60^0\end{cases}}\)

\(\widehat{D}=\dfrac{3}{2}\widehat{B}=\dfrac{3}{2}.60^0=90^0\)

\(\widehat{D}=\dfrac{4}{3}\widehat{C}\Rightarrow\widehat{C}=\dfrac{3}{4}\widehat{D}=\dfrac{3}{4}.90^0=67,5^0\)

\(\widehat{A}=360^0-\widehat{B}-\widehat{C}-\widehat{D}=360^0-60^0-90^0-67,5^0=142,5^0\)

xOy + tOx = 180^o ( kề bù)

xOy + yOz = 180^o ( kề bù) 

mà xOy = xOy. 

=> 2 góc này bằng nhau ( 2 góc cùng kề bù với góc thứ 3 thì bằng nhau).

=> 2 góc đối đỉnh.

like và tim bạn nhé

2 góc cùng kề bù với 1 góc thì = nhau vì:

vd: góc thứ 3 = 80^o thì 2 kề bù với góc 80^o sẽ = 100^o

nghe giống người thứ 3 nhưng không phải nha.

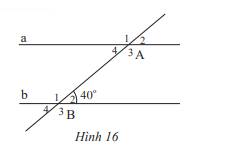
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)

Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)

b) Vì a // b nên:

+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)

+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)

Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ  + \widehat {{B_3}} = 180^\circ  \Rightarrow \widehat {{B_3}} = 180^\circ  - 40^\circ  = 140^\circ \)

c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ  + \widehat {{B_1}} = 180^\circ  \Rightarrow \widehat {{B_1}} = 180^\circ  - 40^\circ  = 140^\circ \)

Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)

Đợi tí xắp xong rồi nha bạn

câu a: góc adc = góc abc+bad

góc adb = góc acb + cad

mà góc bad=cad

suy ra adc-adb=abc-acb

 Câu b: ta có góc adc = góc E+90=góc E+góc E+góc ADB

 suy ra góc E = 1/2 ( góc b - góc c )

ko có hình à bạn