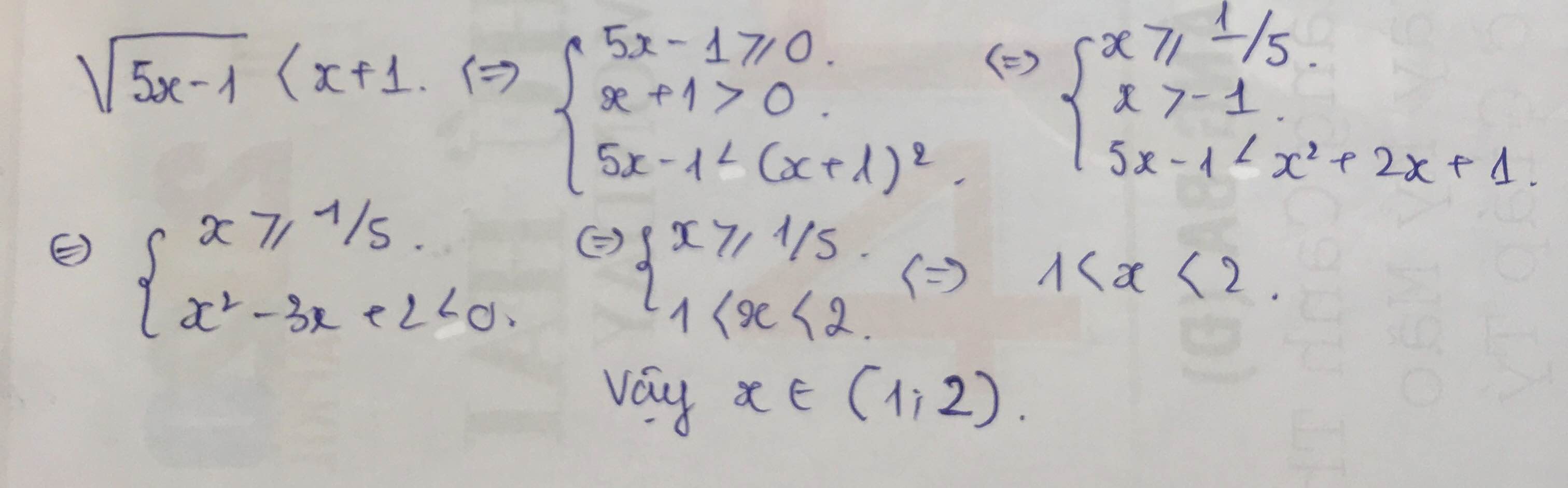Bạn xem bài này nhé: 

http://olm.vn/hoi-dap/question/604325.html

x = 3

\(x^2-x+\sqrt{x+1}-8=0.\)(1) ĐK: x >= -1

Đặt: \(t=\sqrt{x+1}\mid t\ge0\)

Thay vào (1):

(1) \(\Leftrightarrow t^4-3t^2+t-6=0\)

\(\Leftrightarrow t^4-4t^2+t^2-2t+3t-6=0\)

\(\Leftrightarrow\left(t-2\right)\left(t^3+2t^2+t+3\right)=0\)(*)

Vì t>=0 nên t³ + 2t² + t + 3 >0 với mọi t

(*) \(\Leftrightarrow t-2=0\Rightarrow t=2\)

\(\sqrt{x+1}=2\Rightarrow x=3\)(TMĐK >= -1)

Vậy, PT có nghiệm duy nhất x = 3.

\(x-\sqrt{x-8}-3.\sqrt{8}+1=0\)Đúng vậy không? vì cách viết của bạn con 8 đầu có thể nằm ngoài căn

cách giải đề thi chuyên toán 10 năm 2014-2015

a: \(3+\sqrt{2x-3}=x\)

=>\(\sqrt{2x-3}=x-3\)

=>x>=3 và 2x-3=(x-3)^2

=>x>=3 và x^2-6x+9=2x-3

=>x>=3 và x^2-8x+12=0

=>x>=3 và (x-2)(x-6)=0

=>x>=3 và \(x\in\left\{2;6\right\}\)

=>x=6

b: \(\left(\sqrt{x}+1\right)\left(2\sqrt{x}-3\right)-2x=-4\)

=>\(2x-3\sqrt{x}+2\sqrt{x}-3-2x=-4\)

=>\(-\sqrt{x}-3=-4\)

=>\(-\sqrt{x}=-1\)

=>căn x=1

=>x=1(nhận)

c: \(\sqrt{2x+1}-x+1=0\)

=>\(\sqrt{2x+1}=x-1\)

=>x>=1 và (x-1)^2=2x+1

=>x>=1 và x^2-2x+1=2x+1

=>x>=1 và x^2-4x=0

=>x(x-4)=0 và x>=1

=>x=4

\(ĐK:x\ge2\)

\(\sqrt{x+1}=\sqrt{x-2}+1\)

\(\Leftrightarrow x+1=x-1+2\sqrt{x-2}\)

\(\Leftrightarrow2\sqrt{x-2}=2\Leftrightarrow x=3\)