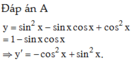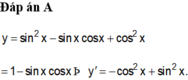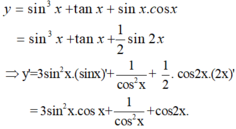Tính đạo hàm hàm số : \(y=\sqrt[10]{\sin3x}\)
Những câu hỏi liên quan
Tính đạo hàm của các hàm số
y
sin
3
x
+
cos
3
x
sin
x
+
cos
x
Đọc tiếp
Tính đạo hàm của các hàm số y = sin 3 x + cos 3 x sin x + cos x
Tính đạo hàm của các hàm số
y
sin
3
x
+
cos
3
x
s
i
n
x
+
c
o
s
x
A.
y
-...
Đọc tiếp
Tính đạo hàm của các hàm số y = sin 3 x + cos 3 x s i n x + c o s x
A. y ' = - cos 2 x + sin 2 x
B. y' = 1
C. y' = 0
D. y ' = - cos 2 x - sin 2 x
Tính y’ và đạo hàm của y’, biết: y = sin 3 x .
y' = (sin3x )' = 3cos3x
y'' = (3 cos3x )' = -9sin3x
Đúng 0
Bình luận (0)
Đạo hàm của hàm số
y
sin
3
x
bằng biểu thức nào sau đây? A.
cos
3
x
2
sin
3
x
B.
3
cos
3
x
2
sin...
Đọc tiếp
Đạo hàm của hàm số y = sin 3 x bằng biểu thức nào sau đây?
A. cos 3 x 2 sin 3 x
B. 3 cos 3 x 2 sin 3 x
C. - 3 cos 3 x 2 sin 3 x
D. - cos 3 x 2 sin 3 x
- Áp dụng công thức: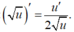 
- Ta có:
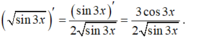
Chọn đáp án B.
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 10:37
Tính đạo hàm của các hàm số sau:
a) \(y = {\left( {2x - 3} \right)^{10}};\)
b) \(y = \sqrt {1 - {x^2}} .\)
\(a,y'=\left[\left(2x-3\right)^{10}\right]'\\ =10\left(2x-3\right)^9\left(2x-3\right)'\\ =20\left(2x-3\right)^9\\ b,y'=\left(\sqrt{1-x^2}\right)'\\ =\dfrac{\left(1-x^2\right)'}{2\sqrt{1-x^2}}\\ =-\dfrac{2x}{2\sqrt{1-x^2}}\\ =-\dfrac{x}{\sqrt{1-x^2}}\)
Đúng 0
Bình luận (0)
Tính các đạo hàm của hàm số sau:
a) \(y=\sqrt{x}\left(x+3\right)\)
b) \(y=\sqrt{2x^2-6x-9}\)
c) \(y=\left(\sqrt{x^2+1}+x\right)^{10}\)
Hàm số
f
x
sin
3
x
có đạo hàm f(x) là: A.
f
(
x
)
−
3
cos
3
x
. B.
f
(
x
)
3
cos
3
x
. C.
f
(...
Đọc tiếp
Hàm số f x = sin 3 x có đạo hàm f'(x) là:
A. f ' ( x ) = − 3 cos 3 x .
B. f ' ( x ) = 3 cos 3 x .
C. f ' ( x ) = − cos 3 x .
Đáp án B
f x = sin 3 x ⇒ f ' x = 3 x ' cos 3 x = 3 cos 3 x
Đúng 0
Bình luận (0)
24 tháng 2 2022 lúc 16:44
cíuuuuuuu em với phần đạo hàm cấp n của các hàm số sau:
1.\(y=sinax\) 2.\(y=cosax\)
\(3.y=sin3x\cdot cosx\) \(4.y=cos5x\cdot cosx\)
Đạo hàm của
y
s
i
n
3
x
+
t
a
n
x
+
s
i
n
x
.
c
o
s
x
là A.
3
s
i
n
2
x
+
1
c
o
s
2
x
+
1...
Đọc tiếp
Đạo hàm của y = s i n 3 x + t a n x + s i n x . c o s x là
A. 3 s i n 2 x + 1 c o s 2 x + 1 2 c o s 2 x
B. 3 s i n 2 x . cos x + 1 c o s 2 x + 2 c o s 2 x
C. 3 s i n 2 x . cos x + 1 c o s 2 x + 2 sin 2 x
D. Đáp án khác
