Cho G là trọng tâm của tam giác ABC;AM là đường trung tuyến,khi đó tỉ số GM/AM là bao nhiêu ?![]()
Cho tam giác ABC,G là trọng tâm của tam giác.Gọi E,F,H lần lượt là trung điểm AG,BG,CG.Chứng minh tam giác EFH đồng dạng tam giác abc và g là trọng tâm của tam giác EFH
Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.
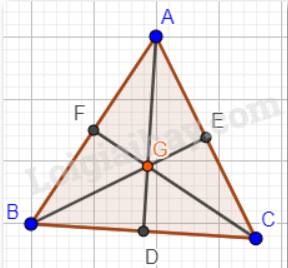
Tam giác ABC đều nên AB = AC = BC.
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD.
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.
Vậy G cũng là trực tâm của tam giác ABC.
Cho tam giác ABC, G là trọng tâm của tam giác. Gọi E,F,H lần lượt là trung điểm của AG, BG, CG. CM tam giác EFH và ABC đồng dạng với nhau và G là trọng tâm tam giác EFH
đếch nói đấy làm sao làm gì được nhau
Cho tam giác ABC, trung tuyến AM, G là trọng tâm tam giác ABC. Gọi D và N lần lượt là trọng tâm của tam giác AMB và tam giác AMC. Chứng minh rằng 3 điểm D;G;N thẳng hàng?
ta gọi AH,AK là 2 đường trung tuyến của tam giác ABM và AMC
ta có D,G,N lần lượt là trọng tâm tam giác ABM,ABC,AM
=> \(\frac{AD}{AH}=\frac{AG}{AM}=\frac{AN}{AK}=\frac{2}{3}\) (tính chất trọng tâm)
=> DG//BC(đingj lí ta lét) và GN//BC(định lí ta lét )
=> D,G,N thẳng hàng(ĐPCM)
bạn ơi xem lại đề đi sao M lại là trọng tâm của tam giác AMB?
Cho tam giác ABC trên cạnh BC lấy D,E sao cho BD=CE(BD<BE). Gọi G là trọng tâm tam giác ABC. CM G cũng là trọng tâm tam giác ADE
Cho tam giác ABC.Trên BC lấy A1,A2 đối xứng qua trung điểm của BC.Rồi lấy B1,B2,C1,C2 tương tự.Chứng minh G1,G2,G thẳng hàng(G là trọng tâm tam giác ABC,G2 là trọng tâm tam giác A1B1C1,G2 là trọng tâm tam giác A2B2C2)
Cho tam giác ABC, trên cạnh BC lấy điểm D, E sao cho BD=CE (BD<BE). Gọi G là trọng tâm tam giác ABC, chứng minh G cũng là trọng tâm tam giác ADE
VẼ DF VUÔNG GÓC VỚI AB, EG VUÔNG GÓC VỚI AC
BD = CE => SABC = SACE => AB.DF = AC.EG => DF/EG = AC/AB (1)
TAM GIÁC ADF ĐỒNG DẠNG VỚI TAM GIÁC AEG => DF/EG = AD/AE (2)
TỪ (1) VÀ (2) => AC/AB = AD/AE, CHO TA TAM GIÁC ABE ĐỒNG DẠNG VỚI TAM GIÁC ACD
=> GÓC ABE = GÓC ACD => TAM GIÁC ABC CÂN (đpcm)
tự vẽ hình
cho tam giác abc có trọng tâm g trung điểm của ga gb gc lần lượt là m n p phép vị tâm g biến tam giác abc thành tam giác mnp có tỉ số là?
Cho tam giác ABC, M là trung điểm của BC. D là điểm bất kì trên tia đối của tia BA. Gọi H và K lần lượt là hình chiếu của B và C trên đường thẳng DM. Gọi G là trọng tâm của tam giác ABC. Chứng minh G là trọng tâm của tam giác AHK
Cho tam giác ABC có trung tuyến AM. Gọi H là trực tâm, O là giao điểm các đường trung trực của tam giác ABC. Giao điểm của AM và HO là G. Chứng minh rằng G là trọng tâm của tam giác ABC