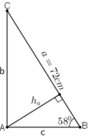
+ Ĉ + B̂ = 90º ⇒ Ĉ = 90º - B̂ = 90º – 58º = 32º

+ b = a.sinB = 72 . sin 58º ≈ 61,06 cm

+ c = a . cos B = 72 . cos 58º ≈ 38,15cm

+ ha = c . sin B = 38,15 . sin 58º = 32,36 cm.

a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ

cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2

TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2  ÁP DỤNG PITA GO TÌM RA CẠNH bc 

b,

sao lại \(\frac{1}{\sqrt{2}}\) ?

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=4^2+5^2=41\)

hay \(BC=\sqrt{41}\left(cm\right)\)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{4^2}{\sqrt{41}}=\dfrac{16\sqrt{41}}{41}\left(cm\right)\\CH=\dfrac{5^2}{\sqrt{41}}=\dfrac{25\sqrt{41}}{41}\left(cm\right)\end{matrix}\right.\)

c) Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:

\(AH^2+HB^2=AB^2\)

\(\Leftrightarrow AH^2=4^2-\left(\dfrac{16\sqrt{41}}{41}\right)^2=\dfrac{400}{41}\)

hay \(AH=\dfrac{20\sqrt{41}}{41}\left(cm\right)\)

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC

 => AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.

Tam giác ANB vuông tại A có AN²+AB²=BN² (Theo Pytago)   mà BN=9cm (gt)

=>AN²+AB²=81        Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC²+AB²=81     (1)

Tam giác ABC vuông tại A có: AC²+AB²=BC² => BC² - AB² = AC²   (2)

Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC² - AB²)+AB²=81       mà BC=12(cmt)

=> 36 - \(\frac{1}{4}\)AB²+AB²=81

=> 36+\(\frac{3}{4}\)AB²=81

=> AB²=60=>AB=\(\sqrt{60}\)

C2

Cho hình thang cân ABCD có đáy lớn CD = 1

C4

Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

Bài 1: 

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow AC^2=15^2-9^2=144\)

hay AC=12(cm)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:

\(AH^2+HB^2=AB^2\)

\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)

hay AH=7,2(cm)

Xét \(\Delta\)ABC có : 

AH² = BH.CH 

AH² = c'.b' (1)

Mà c'/b' = 1/3 

=》3c' = b 

Thay vào (1) ta có : 

12 = c'.3c' 

12 = 3c'² 

c'² = 4 

=》 c' = 2 (cm)

=》b' = 3.2 = 6(cm)

=》 BC = 2 + 6 = 8 (cm)

Ta có : AB² = BH.BC = 2.8 = 16 

=》 AB = 4(cm)

Lại có AC² = CH.BC = 6.8 = 48(cm)

=》 AC = 4\(\sqrt{ }\)3 (cm)

Áp dụng định lí pi ta go 

=> AB² + AC² = 289

Mà \(\dfrac{AB}{AC}\) = \(\dfrac{8}{15}\)=> (\(\dfrac{AB}{AC}\))² = \(\dfrac{64}{225}\)

=> AC²=225 => AC = 15 => AB = 8

Ta có: AB.AC=BC . AH

=> AH = 120/17=7.06

=>BH = 3.76

=> CH = 13.24

Đúng thì like giúp mik nha bạn. Thx bạn