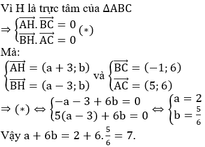Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trực tâm H(-1;3), tâm đường tròn ngoại tiếp I(-3;3), chân đường cao kẻ từ đỉnh A là điểm K(-1;1). Tìm tọa độ các đỉnh A, B, C

Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 1), B(4; 13), C(5; 0). Tọa độ trực tâm H của tam giác ABC là
A.(2; 2)
B. (1; 1)
C.( -2; -2)
D. (-1; -1)
A B → = 3 ; 12 , A C → = 4 ; − 1 ⇒ ( A B ) ⃗ . ( A C ) ⃗ = 3 . 4 + 12 . ( - 1 ) = 0 ⇒ ∆ A B C vuông tại A. Trực tâm của tam giác là đỉnh A. Chọn B
Đúng 0
Bình luận (0)
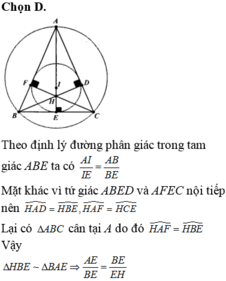
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC cân tại A(0;7) tâm đường tròn nội tiếp là điểm I(01). Gọi E là trung điểm của BC, H là trực tâm tam giác ABC. Biết AH7HE và B có hoành độ âm. Tính xB+2xC A.1 B.
3
2
C.2 D.
2
2
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC cân tại A(0;7) tâm đường tròn nội tiếp là điểm I(01). Gọi E là trung điểm của BC, H là trực tâm tam giác ABC. Biết AH=7HE và B có hoành độ âm. Tính xB+2xC
A.1
B. 3 2
C.2
D. 2 2
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(2;1), trực tâm H(14;-7) đường trung tuyến kẻ từ đỉnh B có phương trình (d):
9x - 5y - 7=0. Tìm tọa độ các đỉnh B, C.
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(-4;1), B(-1;4), C(3;-2) Tìm tọa độ trực tâm của tam giác ABC
1, Trong mặt phẳng Oxy cho tam giác ABC có A(1;6) trực tâm H(1;2) tâm đường tròn ngoại tiếp tam giác là I(2;3) .Tìm tọa độ B,C biết B có hoành độ dương
Lời giải:
Gọi \(B(a,b)\) và \(C(c,d)\)
Ta có \(\overrightarrow {HA}=(0,4)\perp \overrightarrow{BC}=(c-a,d-b)\Rightarrow 4(d-b)=0\rightarrow b=d\)
Thay \(d=b\):
\(\overrightarrow{HB}=(a-1,b-2)\perp \overrightarrow{AC}=(c-1,b-6)\)
\(\Rightarrow (a-1)(c-1)+(b-2)(b-6)=0\)
Lại có \(IA^2=IB^2=IC^2\leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b-3\right)^2=10\\\left(c-2\right)^2+\left(b-3\right)^2=10\end{matrix}\right.\)
\(\Rightarrow (a-2)^2=(c-2)^2\rightarrow a+c=4\) ( \(a\neq c\) )
Ta thu được
\(\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b-3\right)^2=10\\\left(3-a\right)\left(a-1\right)+\left(b-2\right)\left(b-6\right)=0\end{matrix}\right.\)
\(\left\{\begin{matrix} a^2+b^2-4a-6b+3=0\\ -a^2+4a+b^2-8b+9=0\end{matrix}\right.\Rightarrow 2b^2-14b+12=0\rightarrow b=1\)
hoặc \(b=6\)
Thay vào PT suy ra \(\left[{}\begin{matrix}-a^2+4a+2=0\\-a^2+4a-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}a=2+\sqrt{6}\\a=1;a=3\end{matrix}\right.\)
Vậy.....
Đúng 0
Bình luận (1)
Trong mặt phẳng tọa đọ Oxy cho tam giác ABC có
A
(
-
3
;
0
)
,
B
(
3
;
0
)
,
C
(
2
;
6
)
....
Đọc tiếp
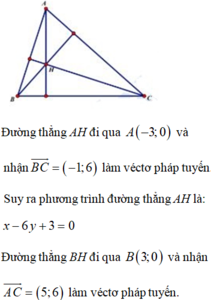
Trong mặt phẳng tọa đọ Oxy cho tam giác ABC có A ( - 3 ; 0 ) , B ( 3 ; 0 ) , C ( 2 ; 6 ) . Gọi H(a;b) là tọa độ trực tâm của tam giác đã cho. Tính a + 6b.
A. a + 6b = 5.
B. a + 6b = 6.
C. a + 6b = 7.
D. a + 6b = 8.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-3;0), B(3;0) và C(2;6). Gọi H(a; b) là trực tâm của tam giác ABC. Tính 6ab A. 10 B.
5
3
C. 60 D. 6
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-3;0), B(3;0) và C(2;6). Gọi H(a; b) là trực tâm của tam giác ABC. Tính 6ab
A. 10
B. 5 3
C. 60
D. 6
Câu 4.(2 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A 1;3 , B 2;1,C0;3 a). Tìm tọa độ trọng tâm tam giác ABC. b). Viết phương trình tổng quát đường trung trực của tam giác ABC. c). Tính khoảng cách từ A đến đường thẳng : x − y + 1 = 0
a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)