Cho tam giác ABC cân tại A ,AB=AC=b ,góc A=2\(\alpha\)
a. Cm: S\(\Delta ABC\)=\(\frac{1}{2}b^2\sin2\alpha\)
b. Cm: \(\sin2\alpha=2\sin\alpha\cos\alpha\)
Cho tam giác ABC có trung tuyến AM, \(\widehat{AMB}=\alpha\), AC=b, AB=c, S là diện tích tam giác ABC. Chứng minh rằng với \(0^0< \alpha< 90^0\)thì b>c
Cho tam giác ABC, widehat{A} alpha( 0 độ alpha 90 độ)Phân giác BD, CN cắt nhau tại O. Phân giác góc ngoài đỉnh B cắt tia CN tại E. Phân giác góc ngoài đỉnh C cắt tia BD tại F.1.Tính widehat{BOC}2.CMR: widehat{BEC}widehat{BFCfrac{alpha}{2}}3.EB cắt FC tại K.CMR: widehat{BOC,}widehat{K}là hai góc kề bù nhau. mik cần gắp lắm-----ai nhanh mik tick cho ha_____mơn nhìu
Đọc tiếp
Cho tam giác ABC, \(\widehat{A}\) = \(\alpha\)( 0 độ < \(\alpha\) < 90 độ)
Phân giác BD, CN cắt nhau tại O. Phân giác góc ngoài đỉnh B cắt tia CN tại E. Phân giác góc ngoài đỉnh C cắt tia BD tại F.
1.Tính \(\widehat{BOC}\)
2.CMR: \(\widehat{BEC}=\widehat{BFC=\frac{\alpha}{2}}\)
3.EB cắt FC tại K.
CMR: \(\widehat{BOC,}\widehat{K}\)là hai góc kề bù nhau.
mik cần gắp lắm-----ai nhanh mik tick cho ha_____mơn nhìu
Cho tam giác ABC có A=\(\alpha\)( 0<\(\alpha\)< 1800) , I là giao điểm của hai tia phân giác của hai góc B và C .Tính số đo góc BIC theo\(\alpha\)trong mỗi trường hợp sau:
a, Góc B và C là 2 góc trong của tam giác ABC
b,Góc B và C là 2 góc ngoài của tam giác ABC
Ai nhanh mk tick
Cho \(\Delta\)ABC cân tại A có góc A=\(\alpha\)độ. (120<\(\alpha\)<180). Lấy điểm M trong tam giác sao cho góc MCA= MAC = \(\frac{\alpha-60}{2}\)độ. (M và A khác phía BC). tính góc BMA.
Chứng minh rằng với mọi góc \(\alpha \;\;({0^o} \le \alpha \le {180^o})\), ta đều có:
a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\)
c) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\)
d) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\)
a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
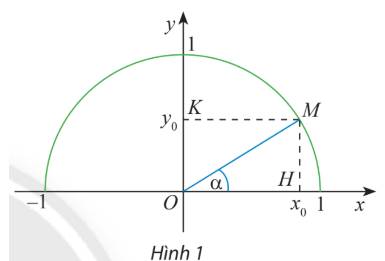
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
Đúng 0
Bình luận (0)
cho tam giác abc có A =alpha (0<alpha<180).I là giao điểm của các tia phân giác tại B và C .tính BIC theo alpha.Tim alpha biet BIC=2BAC
16 tháng 8 2020 lúc 8:32
Cho tam giác ABC vuông tại A, góc C = \(\alpha< 90^o\) . Chứng minh rằng:
\(tan_{2\alpha}=\frac{2tan_{\alpha}}{1-tan^2_{\alpha}}\)
Cho tam giác ABC vuoong tại A có C\(=\alpha\)\(\left(\alpha< 45^0\right)\), BC=a. Vẽ trung tuyến AM.Qua A vẽ đg vuôn góc AM cắt BC tại N.C/m \(CN=\frac{a^2.cos^2\alpha}{2cos^2\alpha-1}\)
Cho tam giác ABC, ABAC1, widehat{A}2alphaleft(0 alpha 45right). Vẽ đường cao AD, BEa) Các tỉ số lượng giác sinalpha,cosalpha,sin2alpha,cos2alphađược biểu diễn bởi những đường thẳng nào?b) Chứng minh: tam giác ADC đồng dạng với tam giác BEC, từ đó suy ra các hệ thức:sin2alpha2sinalphacosalphacos2alpha1-2sin^2alpha2cos^2alpha-1cos^2alpha-sin^2alpha
Đọc tiếp
Cho tam giác ABC, AB=AC=1, \(\widehat{A}=2\alpha\left(0< \alpha< 45\right)\). Vẽ đường cao AD, BE
a) Các tỉ số lượng giác \(\sin\alpha,\cos\alpha,\sin2\alpha,\cos2\alpha\)được biểu diễn bởi những đường thẳng nào?
b) Chứng minh: tam giác ADC đồng dạng với tam giác BEC, từ đó suy ra các hệ thức:
\(\sin2\alpha=2\sin\alpha\cos\alpha\)\(\cos2\alpha=1-2\sin^2\alpha=2\cos^2\alpha-1=\cos^2\alpha-\sin^2\alpha\)