cho hình vuông OABC có tâm I (1;2)
tìm tọa độ A,B,C ?
Những câu hỏi liên quan
Trên hình vẽ ta có đường tròn tâm O, bán kính 10cm, tứ giác OABC là hình vuông với A và C nằm trên đường
tròn. Tìm phần diện tích của hình vuông nằm ngoài đường tròn.
Trên hình vẽ ta có đường tròn tâm O, bán kính 10cm, tứ giác OABC là hình vuông với A và C nằm trên đường tròn. Tìm phần diện tích của hình vuông nằm ngoài đường tròn.
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau: I. H là trực tâm của
∆
ABC. II. H là trọng tâm của
∆
ABC. III.
1
O
H
2
1
O
A
2...
Đọc tiếp
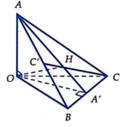
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau:
I. H là trực tâm của ∆ ABC.
II. H là trọng tâm của ∆ ABC.
III. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Số mệnh đề đúng là:
A. 0
B. 1
C. 2
D. 3
Đáp án C.
Từ (1) và (2) suy ra
=> AH là đường cao trong tam giác BCD
Tương tự suy ra, CH là đường cao trong tam giác BCD => H là trực tâm => I đúng => II sai
+ Gọi 
=> 1 O H 2 = 1 O B 2 + 1 O C 2 => 1 O H 2 = 1 O A ' 2 + 1 O A 2 = 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
=> III đúng
Đúng 0
Bình luận (0)
Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Nếu I là hình chiếu của điểm O trên mặt phẳng (ABC) thì I là:
A. trọng tâm của tam giác ABC.
B. trực tâm của tam giác ABC.
C. tâm của đường tròn ngoại tiếp tam giác ABC.
D. tâm của đường tròn nội tiếp tam giác ABC.
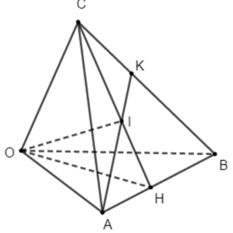
Giả sử AI và CI cắt CB và AB tại K và H
⇒ AB ⊥ (OCH) ⇒ AB ⊥ CH
Chứng minh tương tự ta cũng có CB ⊥ AK ⇒ I là trực tâm của tam giác ABC
Đáp án B
Đúng 0
Bình luận (0)
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau:I. H là trực tâm của tam giác ABC.II. H là trọng tâm của tam giác ABC.III.
1
O
H
2
1
O
A
2
+
1
O
B...
Đọc tiếp
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau:
I. H là trực tâm của tam giác ABC.
II. H là trọng tâm của tam giác ABC.
III. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Số mệnh đề đúng là
A. 0
B. 1
C. 2
D. 3
Cho tứ diện OABC có OA, OB, OC vuông góc từng đôi một. Gọi H là hình chiếu vuông góc của O trên (ABC). CMR:
a/ BC vuông góc (OAH)
b/ H là trực tâm tam giác ABC
c/ 1/OH^2=1/OA^2 + 1/ OB^2 + 1/OC^2
d/ Các góc của tam giác ABC đều nhọn
e/ Tìm tập hợp các điểm M trong không gian sao cho MA^2 + MB^2 + MC^2 = 3MO^2
Cho tứ diện OABC có OA, OB , OC đôi một vuông góc với nhau a, CM: OA vuông góc với (OBC) b, gọi OK,OH lần lượt là đường cao của ∆OBC và ∆OAK. CM : OH vuông góc với (ABC) c, H là trực tâm của ∆ABC
a: OA\(\perp\)OB
OA\(\perp\)OC
OB,OC cùng thuộc mp(OBC)
Do đó: OA\(\perp\)(OBC)
b: Ta có: BC\(\perp\)AK
BC\(\perp\)AO
AK,AO cùng thuộc mp(AKO)
Do đó: BC\(\perp\)(AKO)
=>BC\(\perp\)OH
Ta có: OH\(\perp\)BC
OH\(\perp\)AK
AK,BC cùng thuộc mp(ABC)
Do đó: OH\(\perp\)(ABC)
Đúng 0
Bình luận (0)
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng :
a) H là trực tâm của tam giác ABC
b) \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}+\dfrac{1}{OC^2}\)
Cho hình vuông ABCD có tọa độ đỉnh A(1;2) và tâm hình vuông là I(-1; -4). Khi đó phương trình của đường chéo BD là:
A. x + 3y + 13 = 0
B. 3x – y + 1 = 0
C. x – y – 3 = 0
D. x + y + 5 = 0
