cho hình bình hành ABCD . Tìm tập hợp các điểm M sao cho : MA2 + MB2 + MC2 + MD2 = k2 , trong đó k là một số cho trước

Những câu hỏi liên quan
Cho hình vuông ABCD cạnh a . Tìm tập hợp M sao cho :
2 MA2 + MB2 = MC2 + MD2
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:
M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị cực tiểu.
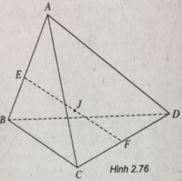
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
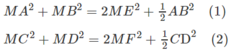
Cộng (1) và (2) ta có:
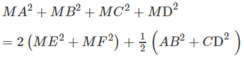
Gọi J là trung điểm của EF, ta có:
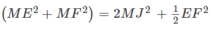
Khi đó:
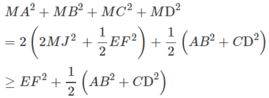
Vậy M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị nhỏ nhất khi M ≡ J.
Đúng 0
Bình luận (0)
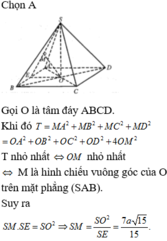
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng A.
7
a...
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng T = M A 2 + M B 2 + M C 2 + M D 2 nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng
A. 7 a 15 15
B. a 15 2
C. a 15 3
D. 4 a 15 15
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng T = M A 2 + M B 2 + M C 2 + M D 2 nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng


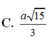
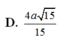
Cho A(1; 2), B(-3; 1) và C(4; -2). Tìm tập hợp các điểm M sao cho MA2 + MB2= MC2
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.
Đúng 0
Bình luận (0)
Bài 1. Cho hình chữ nhật ABCD, M là một điểm bất kì thỏa mãn AMB ̂ =900
. Chứng minh rằng MA2 + MB2 + MC2 + MD2 không đổi
Bài 2. Cho đường tròn (O,R), P là điểm cố định nằm trong đường tròn.
Qua P kẻ 2 dây cung AB và CD vuông góc với nhau.
1) Chứng minh PA2 + PB2 + PC2 + PD2 không đổi
2) Gọi M là trung điểm của AC. Chứng minh PM vuông góc với BD
Trong không gian toạ độ Oxyz cho 3 điểm
A
0
;
2
;
1
;
B
1
;
0
;
2
;
C
2
;
1
;
−
3
.
Tập hợp các điểm thoã mãn...
Đọc tiếp
Trong không gian toạ độ Oxyz cho 3 điểm A 0 ; 2 ; 1 ; B 1 ; 0 ; 2 ; C 2 ; 1 ; − 3 . Tập hợp các điểm thoã mãn M A 2 + M B 2 + M C 2 = 20 là một mặt cầu. Bán kính mặt cầu đó là.
A. R = 2
B. R = 6 2
C. R = 6 3
D. R = 2 5
Đáp án C.
G(1;1;0) là trọng tâm tam giác ABC
Ta có G A ¯ + G B ¯ + G C ¯ = 0 → .
Khi đó M A 2 + M B 2 + M C 2 = M A ¯ 2 + M B ¯ 2 + M C ¯ 2
= M G ¯ + M A ¯ 2 + M G ¯ + G B ¯ 2 + M G ¯ + G C ¯ 2
⇔ 3 M B 2 + M G ¯ G A ¯ + G B ¯ + G C ¯ + G A 2 + G B 2 + G C 2 = 20
M G 2 = 20 − G A 2 − G B 2 − G C 2 3 = 3 2
⇒ tâm G 1 ; 1 ; 0 và R = 6 3 .
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
A.
3...
Đọc tiếp
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T = M A 2 + M B 2 + M C 2 + M D 2
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
. A.
3
a
2...
Đọc tiếp
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng T = M A 2 + M B 2 + M C 2 + M D 2 .
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Đáp án D
Với tứ diện đều ABCD thì mặt cầu (S) là mặt cầu có tâm trùng với tâm của mặt cầu ngoại tiếp tứ diện ABCD và là trọng tâm của tứ diện đều cạnh a, đồng thời có bán kính R = a 2 4
Gọi G là trọng tâm của tứ diện ⇒ G A ¯ + G B ¯ + G C ¯ + G D ¯ = 0 ¯
Ta có:
T = M A 2 + M B 2 + M C 2 + M D 2 = M G ¯ + G A ¯ 2 + M G ¯ + G B ¯ 2 + M G ¯ + G C ¯ 2 + M G ¯ + G D ¯ 2
= 4 M G 2 + 2 M G ¯ G A ¯ + G B ¯ + G C ¯ + G D ¯ ⏟ 0 + G A 2 + G B 2 + G C 2 + G D 2 = 4 M G 2 + 4 G A 2
= 4 a 2 4 2 + 4 a 6 4 2 = 2 a 2 . Vậy T = M A 2 + M B 2 + M C 2 + M D 2 = 2 a 2
Đúng 0
Bình luận (0)