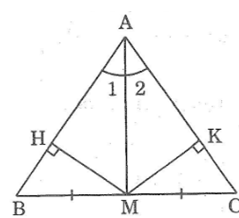
Cho mình hỏi : Trong tam giác cân , đường trung tuyến đồng thời là đường phân giác đúng kh ạ ?

Những câu hỏi liên quan
Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Gợi ý: Trong ΔABC, nếu AD là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn DA1, sao cho DA1 = AD.
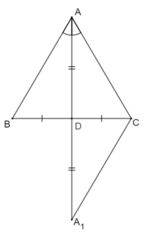
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)

⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 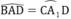 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
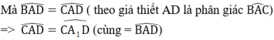
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Đúng 0
Bình luận (0)
cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng Minh tam giác ABC cân
Xét ΔABC có
AM là đường trung tuyến
AM là đường phân giác
Do đó: ΔABC cân tại A
Đúng 3
Bình luận (0)
\(\text{Xét }\Delta ABC\text{ có:}\)
\(\left\{{}\begin{matrix}AM\text{ là đường phân giác(gt)}\\AM\text{ là đường trung tuyến(gt)}\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\text{ cân tại A}\)
Đúng 1
Bình luận (0)
Tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh rằng tam giác đó là tam giác cân.
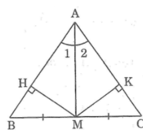
Kẻ MH ⊥ AB, MK ⊥ AC
Vì AM là tia phân giác của ∠(BAC) nên MH = MK (tính chất tia phân giác)
Xét hai tam giác MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90º
MH = MK (chứng minh trên)
MB = MC (gt)
Suy ra: ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.
Đúng 0
Bình luận (0)
Chứng minh định lí : Nếu tam giác có 1 đường trung tuyến đồng thời là đường phân giác thì tam giác đó là 1 tam giác cân.
Gợi ý: Trong tam giác ABC , nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
câu 1 :đúng hay sai
a)hai tam giác bằng nhau thì hai đường trung tuyến tương ứng bằng nhau
b)hai tam giác bằng nhau thì hai đường phân giác tương ứng bằng nhau
c)hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau
d)trong tam giác cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường phân giác , đường cao, đường trung trực
Câu 1: chứng minh nếu tam giác có 1 đường trung tuyến đồng thời là đường cao thì tam giác đó là tam giác cânCâu 2: Chứng minh nếu tam giác có 1 đường trung trực đồng thời là đường cao thì tam giác đó là tam giác câncâu 3: Chứng minh nếu tam giác có 1 đường trung trực đồng thời là đường phân giác thì tam giác đó là tam giác cânCâu 4: Chứng minh nếu tam giác có 1 đường phân giác đồng thời là đường cao thì tam giác đó là tam giác cân
Đọc tiếp
Câu 1: chứng minh " nếu tam giác có 1 đường trung tuyến đồng thời là đường cao thì tam giác đó là tam giác cân"
Câu 2: Chứng minh " nếu tam giác có 1 đường trung trực đồng thời là đường cao thì tam giác đó là tam giác cân"
câu 3: Chứng minh " nếu tam giác có 1 đường trung trực đồng thời là đường phân giác thì tam giác đó là tam giác cân"
Câu 4: Chứng minh " nếu tam giác có 1 đường phân giác đồng thời là đường cao thì tam giác đó là tam giác cân"
Câu 1:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
DB= DC
=> tam giác ABD = tam giác ACD (2 cạnh góc vuông)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 2:
Chứng minh y chang câu 1
Câu 3:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
BAD = CAD
=> tam giác ABD = tam giác ACD (cạnh góc vuông_ góc nhọn)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 4:
Chứng minh giống hệt câu 3.
Đúng 1
Bình luận (0)
Tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh rằng tam giác đó là tam giác cân ?
Khi một tam giác có đường trung tuyến đồng thời là đường phân giác thì đó là tam giác cân.
Ở đây tam giác ABC có AM là trung tuyến đồng thời là phân giác vậy
=> tam giác ABC là tam giác cân (tính chất tam giác cân)
Đúng 1
Bình luận (0)
Ta có hình vẽ :
Trên tia đổi của tia MA lấy điểm H sao cho MA=MH
Xét \(\Delta MBH\) và \(\Delta MCA\) có:
\(\left\{{}\begin{matrix}AM=HM\left(theocachve\right)\\\widehat{BMH}=\widehat{CMA\left(\text{đ}^2\right)}\\BM=CM\left(AMlatrungtuyen\right)\end{matrix}\right.\)
=> \(\Delta MBH\) = \(\Delta MCA\) (c.g.c)
=> +) BH=CA ( hai cạnh tương ứng) (1)
+) \(\widehat{BHM}=\widehat{CAM}\) ( hai góc tương ứng ) (2)
Ta lại có:
AM là phân giác => \(\widehat{BAM}=\widehat{MAC}\) (3)
Từ (2) và (3) suy ra: \(\widehat{BAM}=\widehat{MHB}\)
=> \(\Delta HBA\) là tam giác cân ( vì có hai góc ở đáy bằng nhau )
=> AB=HB ( hai cạnh bên của tam giác cân ) (4)
Từ (1) và (4) suy ra :
AB=AC
=> \(\Delta ABC\) là tam giác cân ( vì có hai cạnh trong tam giác bằng nhau )
( đ.p.c.m )
Đúng 2
Bình luận (0)
Kẻ MH ⊥ AB, MK ⊥ AC
Vì AM là tia phân giác của ∠(BAC) nên MH = MK (tính chất tia phân giác)
Xét hai tam giác MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 900
MH = MK (chứng minh trên)
MB = MC (gt)
Suy ra: ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.
Đúng 1
Bình luận (0)
Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
Gợi ý : Trong ∆ABC, nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn AD1 sao cho DA1 = AD
MÔN ĐẠI CƯƠNGÔN THI ĐẠI HỌCTOÁN HỌCNGỮ VĂNANH VĂNVẬT LÝHÓA HỌCSINH HỌCLỊCH SỬĐỊA LÝTRUYỆN CỔ TÍCHSóng - Xuân Quỳnh  Đàn ghi ta của Lor-ca - Thanh Thảo
Đàn ghi ta của Lor-ca - Thanh Thảo 
TOÁN HỌCToán lớp 7
Bài 42 trang 73 sgk toán lớp 7- tập 2
Cập nhật lúc: 08/07/2014 17:21 pm Danh mục: Toán lớp 7
Chứng minh định líBài 38 trang 73 sgk toán lớp 7- tập 2Bài 40 trang 73 sgk toán lớp 7- tập 2Bài 36 trang 72 sgk toán lớp 7- tập 2Bài 42 trang 73 sgk toán lớp 7- tập 2Bài 39 trang 73 sgk toán lớp 7- tập 2Xem thêm: Tính chất ba đường phân giác của tam giác
42. Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
Gợi ý : Trong ∆ABC, nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn AD1 sao cho DA1 = AD
Hướng dẫn:
Giả sử ∆ABC có AD là phân giác và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD

Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên
mà (gt)
=>
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
Đúng 0
Bình luận (0)
Chứng minh : trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến ứng với cạnh đáy.
Để mik giúp bạn nha Ngọc Hàn Băng Nhi!
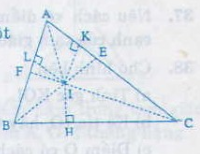
GT : ∆ABC
Hai phân giác BE, CF cắt nhau tại I
AI là tia phân giác của góc A
KL: IH = IK = IL
- Vì I nằm trên tia phân giác BE của góc B nên IL = IH (1) (theo định lí 1 về tính chất của tia phân giác).- Tương tự, ta có IK = IH (2).
- Từ (1) và (2) suy ra IK = IL (= IH), hay I cách đều hai cạnh AB, AC của góc A. Do đó I nằm trên tia phân giác của góc A (theo định lí 2 về tính chất của tia phân giác), hay AI là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
Tóm lại, ba đường phân giác của tam giác ABC cùng đi qua điểm I và điểm này cách đều ba cạnh của tam giác, nghĩa là : IH = IK = IL.
Đây là chỉ là hướng dẫn thui( Do gõ nhìu mỏi tay wá!) Có gì bạn tự triểm khai ra nhé! Chúc bạn học tốt!
Đúng 0
Bình luận (4)
Vì tam giác ABC cân tại A nên góc ABC= góc ACB(theo tính chất của tam giác cân)
Xét tam giác ABD và tam giác ACD ta có:
góc BAD=góc CAD(gt); AB=AC(gt); góc ABD=góc ACD(cmt)
Do đó tam giác ABD= tam giác ACD(g.c.g)
=> BD=CD=> AD là trung tuyến của cạnh BC của tam giác ABC(đpcm)
Chúc bạn học tốt!!!
Đúng 0
Bình luận (0)