Vẽ đồ thị hàm số y=2x-3 và y=x+5

Những câu hỏi liên quan
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
a) khảo sát và vẽ đồ thị hàm số \(y=x^4-2x^2+3\)
b) vẽ đồ thị hàm số \(y=\left|x^4-2x^2+3\right|\)
Biết rằng đồ thị hàm số y = f(x) = 2x + 5 và đồ thị hàm số y = f(x) = x + 3 cắt nhau tại điểm M. Không vẽ đồ thị, hãy tìm tọa độ của điểm M.
M thuộc đồ thị hs y = 2x + 5 => yM = 2xM + 5
M thuộc đths y = x + 3 => yM = xM+ 3
=> 2xM + 5 = xM + 3 => 2xM - xM = 3 -5 => xM = -2
=> yM = xM + 3 = -2 + 3 = 1
Vậy M(1;-2)
Đúng 1
Bình luận (0)
Cho hàm số y = x + căn 3 và y=2x - căn 5. Vẽ đồ thị hàm số trên cùng một mặt phẳng toạ độ
Ai giải cho mình đi vì nó căn 3 với căn 5 nên mình ko biết lặp bảng thế nào
Đúng 0
Bình luận (0)
Cho hai hàm số bậc nhất : y=2x+5 và y =x+3 A) vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ . b) tìm tọa độ giao điểm của đồ thị trên . c) tìm m để đường thẳng y=3x+m-3 đồng quy với đồ thị hai hàm số trên.
b: Tọa độ giao là:
2x+5=x+3 và y=x+3
=>x=-2 và y=1
c: Thay x=-2 và y=1 vào (d), ta được:
m-3-6=1
=>m=10
Đúng 0
Bình luận (0)
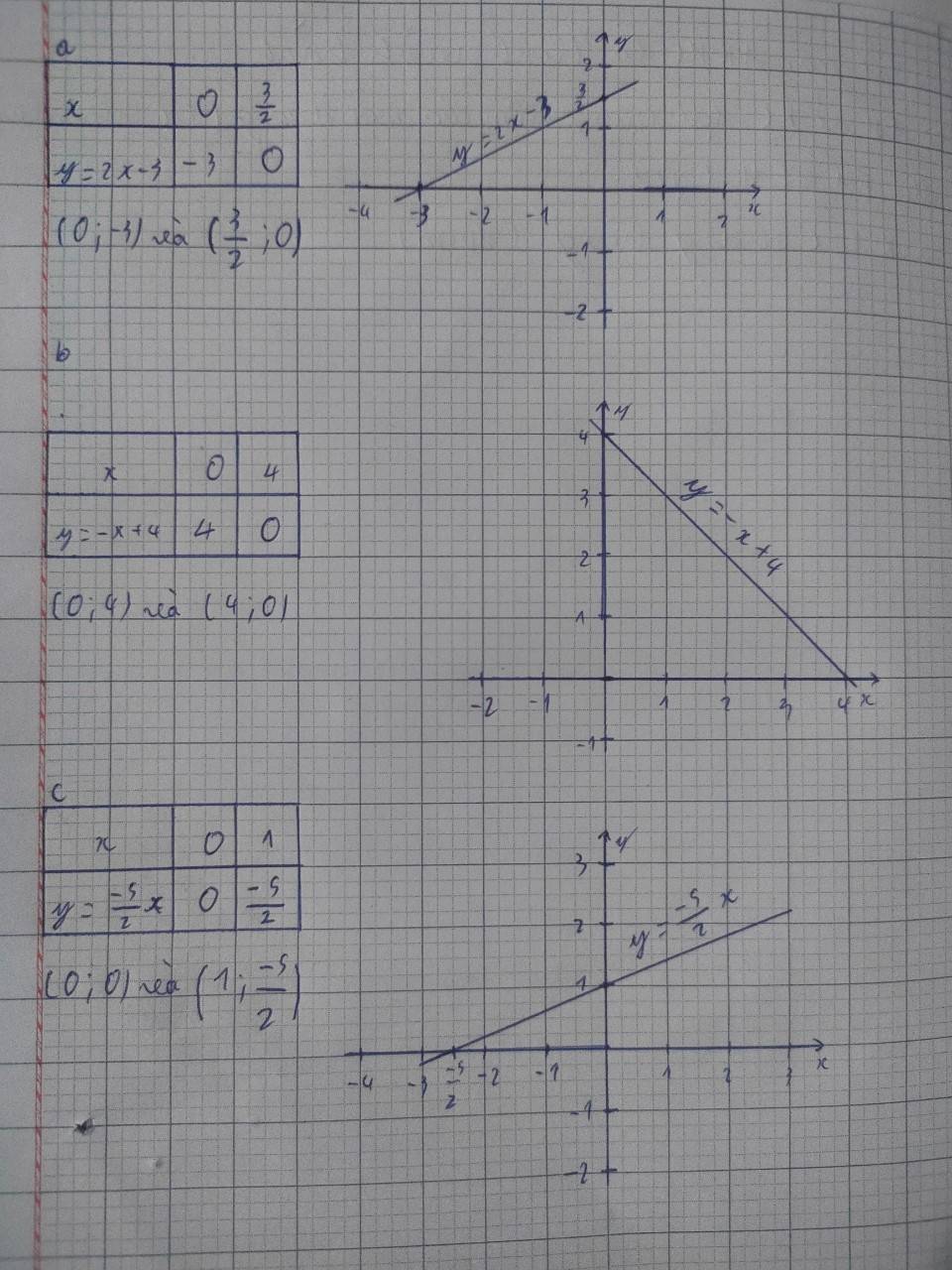
3.vẽ đồ thị hàm số sau: a/ y =2x- 3 b/ y = -x+4 c/ y = -5/2x
Cho 2 hàm số y = f(x) = 2x + 5 và y = g(x) = x + 3. Tính toạ độ M là giao điểm của 2 đồ thị (không vẽ đồ thị)
Xem thêm câu trả lời
Câu 3: Cho các hàm số \(y=2x+5\) và \(y=-x+2\)
a. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng toạ độ Oxy.
b. Dựa vào hình vẽ, xác định toạ độ giao điểm A của hai đồ thị hàm số.
c. Hai đồ thị của hai hàm số đã cho cắt trục hoành tại các điểm B và C. Tính diện tích tam giác ABC
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
Đúng 1
Bình luận (0)