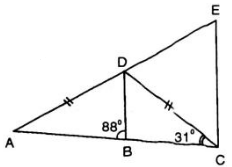
Cho tam giác cân ABC \(\widehat{A}=110^0\). Trên cạnh BC lấy điểm D biết \(\widehat{ADC}=105^0\). Từ C kẻ đường thẳng song song với AD cắt BA ở E. So sánh các cạnh của tam giác BEC.
Hình 61 cho biết a // b, \(\widehat{C}=44^0;\widehat{D}=132^0\)
Tính số đo góc COD

(Hướng dẫn : Vẽ đường thẳng song song với đường thẳng a và đi qua điểm O)
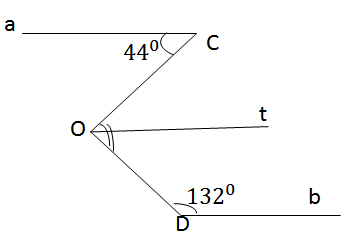
Vẽ tia Ot // a (Ca, Ot nằm ở hai nửa mp đối nhau có bờ OC).
Mà a // Ot
=>
(hai góc trong cùng phía)
Suy ra:
Vậy
Đúng 0
Bình luận (0)
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : widehat{A}+widehat{B}200^{^0};widehat{B}+widehat{C}218^0;widehat{C}+widehat{D}160^0 TÍNH widehat{C}VÀ widehat{D}BÀI 2 : CHO TỨ GIÁC ABCD CÓ widehat{B}80^0;widehat{D}120^0GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC BÀI 3 : TỨ GIÁC ABCD CÓ widehat{A}57^0;widehat{C}110^0;widehat{D}75^0.TÍNH GÓC NGOÀI TẠI ĐỈNH B
Đọc tiếp
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : \(\widehat{A}+\widehat{B}=200^{^0};\widehat{B}+\widehat{C}=218^0;\widehat{C}+\widehat{D}=160^0\) TÍNH \(\widehat{C}\)VÀ \(\widehat{D}\)
BÀI 2 : CHO TỨ GIÁC ABCD CÓ \(\widehat{B}=80^0;\widehat{D}=120^0\)GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC
BÀI 3 : TỨ GIÁC ABCD CÓ \(\widehat{A}=57^0;\widehat{C}=110^0;\widehat{D}=75^0\).TÍNH GÓC NGOÀI TẠI ĐỈNH B
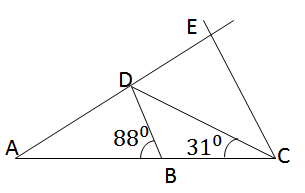
Cho tam giác cân ADC (AD = DC) có \(\widehat{ACD}=31^0\). Trên cạnh AC lấy một điểm B sao cho \(\widehat{ABD}=88^0\). Từ C kẻ một tia song song với BD cắt tia AD ở E
a) Hãy tính các góc DCE và DEC
b) Trong tam gác CDE, cạnh nào lớn nhất ? Tại sao ?
Hướng dẫn làm bài:
a)∆ADC cân tại D, có ˆADC=310=>ˆADC=1800−2.^CADC^=310=>ADC^=1800−2.C^
=> ˆADC=1800−620=1180ADC^=1800−620=1180
+∆ADB có ^A=310,ˆABD=880A^=310,ABD^=880
=> ˆADB=1800−(310+880)ADB^=1800−(310+880)
Hay ˆADB=610ADB^=610
+BD //CE
=> ˆDEC=ˆADB=610DEC^=ADB^=610 (đồng vị)
b) ˆEDCEDC^ là góc ngoài ∆ADC cân tại D
=> ˆEDC=2.^C=620EDC^=2.C^=620
∆DEC có ^E=610;^D=620=>ˆDCE=570E^=610;D^=620=>DCE^=570
Vì 570<610<620=>DE<DC<CE570<610<620=>DE<DC<CE
Vậy CE là cạnh lớn nhất.
Đúng 0
Bình luận (0)
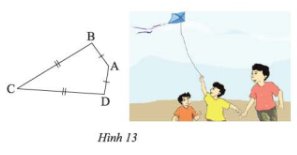
Ta gọi tứ giác ABCD với AB = AD, CB = CD (hình 13) là hình “cái diều”.
a. Chứng minh rằng AC là đường trung trực của BD.
b. Cho biết \(\widehat B = {95^0},\widehat C = {35^0}.\)Tính \(\widehat A\) và \(\widehat D\)
a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AD=DC=CB;\(\widehat{ADC}=110^0;\widehat{BCD}=130^0\)
Tính \(\widehat{ABC}\)
Dựng tứ giác ABCD, biết AB = 2cm, AD = 3cm, \(\widehat{A}=80^0,\widehat{B}=120^0,\widehat{C}=100^0\)
cho 2 góc kề bù \(\widehat{CBA}\)và\(\widehat{DBC}\)với \(\widehat{CBA}=120^0\)
a,tính \(\widehat{DBC}\)
b,trên cùng 1 nửa mặt phẳng AD chứa tia BC vẽ \(\widehat{DBM}=30^0\).tia BM có phải tia phân giác của \(\widehat{DBC}\)ko?vì sao?
a) có \(\widehat{CBA}+\widehat{DBC}=180^o\left(kb\right)\)
\(hay120^o+\widehat{DBC}=180^o\)
\(\Rightarrow\widehat{DBC}=180^o-120^o\)
\(\Rightarrow\widehat{DBC}=60^o\)
b) có \(\widehat{DBM}< \widehat{DBC}\left(30^o< 60^o\right)\)
=> BM nằm giữa hai tia BD và BC
\(\Rightarrow\widehat{DBM}+\widehat{MBC}=\widehat{DBC}\)
\(hay30^o+\widehat{MBC}=60^o\)
\(\Rightarrow\widehat{MBC}=60^o-30^o\)
\(\Rightarrow\widehat{MBC}=30^o\)
mà \(\widehat{DBM}=30^o\)
=> \(\widehat{MBC}=\widehat{DBM}=30^o\)
mà BM nằm giữa hai tia BD và BC
=> BM là tia phân giác của \(\widehat{DBC}\)
Đúng 0
Bình luận (0)
Cho hình thang ABCD ( BC//AD ). Tính các góc của hình thang biết \(\widehat{B}=70^0\), \(\widehat{C}-\widehat{D}=50^0\) ( có vẽ hình )
Trong hình thang vuông ABCD với các đáy là AD, BC có \(\widehat{A}=\widehat{B}=90^0;\widehat{ACD}=90^0;BC=4cm;AD=16cm\). Hãy tìm các góc C và D của hình thang ?