Lời giải:

TXĐ: (-\infty; -1)\cup (-1;+\infty)$
$y'=\frac{1}{(x+1)^2}-2$

$y'>0\Leftrightarrow (x+1)^2< \frac{1}{2}\Leftrightarrow \frac{-1}{\sqrt{2}}-1< x< \frac{1}{\sqrt{2}}-1$

$y'< 0\Leftrightarrow (x+1)^2> \frac{1}{2}\Leftrightarrow x> \frac{1}{\sqrt{2}}-1$ hoặc $x< \frac{-1}{\sqrt{2}}-1$
Vậy hàm số:

Đồng biến trên $(\frac{-1}{\sqrt{2}}-1; \frac{1}{\sqrt{2}}-1)$ và nghịch biến trên $(\frac{1}{\sqrt{2}}-1; +\infty)\cup (-\infty; \frac{-1}{\sqrt{2}}-1)$

ta tính \(y'=3x^2-4x+1\)

\(y'=0\Rightarrow3x^2-4x+1=0\Rightarrow x=1;x=\frac{1}{3}\)

ta có 

ta có trong khoảng 2 nghiệm thì y' cùng dấu với hệ số a, ngoài khoảng 2 nghiệm trái dấu với hệ số a

suy ra f'(x)>0 với \(x\in\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\) suy ra hàm số  đồng biến trên \(\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\)

lại có f'(x)<0 với \(x\in\left(\frac{1}{3};1\right)\) suy ra hàm số nghịch biến trên \(\left(\frac{1}{3};1\right)\)

a: Hàm số này đồng biến vì \(2-\sqrt{3}>0\)

b: \(f\left(2+\sqrt{3}\right)=4-3-1=0\)

\(f\left(\sqrt{3}\right)=2\sqrt{3}-3-1=2\sqrt{3}-4\)

a: y=2x-1

a=2>0

=>Hàm số đồng biến

b: y=-3x+5

a=-3<0

=>Hàm số nghịch biến

c: \(y=\left(\sqrt{3}-\sqrt{2}\right)\cdot x\)

\(a=\sqrt{3}-\sqrt{2}>0\)

=>Hàm số đồng biến

d: \(y=-\dfrac{1}{2}\sqrt{x}+1\)

Vì -1/2<0 nên hàm số nghịch biến

Hàm số y = |x + 1|

Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1.

Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1. 

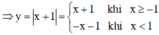
+ Tập xác định: R

+ Trên (–∞; –1), y = x + 1 đồng biến.

Trên (–1 ; +∞), y = –x – 1 nghịch biến.

Ta có bảng biến thiên :

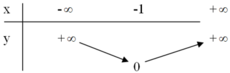
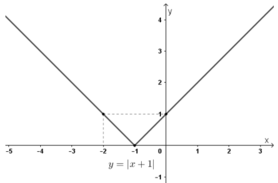
+ Đồ thị hàm số gồm hai phần:

Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1.

Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.

a)

TXĐ: $[-3;3]$

$f'(x)=\frac{-x}{\sqrt{9-x^2}}=0\Leftrightarrow x=0$ (hàm số không có đạo hàm tại $x=\pm 3$)

BBT:

Từ BBT ta thấy hàm số $y$ đồng biến trên khoảng $(-3;0)$ và nghịch biến trên khoảng $(0;3)$

b)

TXĐ: \((-\infty;-4]\cup [1;+\infty)\)

Ta có: \(y'=\frac{2x+3}{2\sqrt{x^2+3x-4}}\).

\(y'=0\Leftrightarrow \left\{\begin{matrix} 2x+3=0\\ x\in (-\infty;-4)\cup (1;+\infty)\end{matrix}\right.\) (vô lý)

Do đó $y'=0$ vô nghiệm.

BBT:

Vậy $y$ nghịch biến trên khoảng $(-\infty; -4)$ và đồng biến trên khoảng $(1;+\infty)$

c)
TXĐ: $[2;4]$

Ta có:

\(y'=\frac{1}{2}\left(\frac{1}{\sqrt{x-2}}-\frac{1}{\sqrt{4-x}}\right)\). Hàm số không có đạo hàm tại $x=2; x=4$

\(y'=0\Leftrightarrow \left\{\begin{matrix} \sqrt{x-2}=\sqrt{4-x}\\ x\in (2;4)\end{matrix}\right.\Leftrightarrow x=3\)

BBT:

Vậy $y$ đồng biến trên khoảng $(2;3)$ và nghịch biến trên khoảng $(3;4)$

Cho hàm số y=(1-√5)x-1
a, Hàm số đồng biến hay nghịch biến trên R?vì sao
Hàm số nghịch biến vi (1-√5<0
b,Tính y khi x=1+√5
y=(1-√5)(1+√5)-1
y = -5