mọi người giải chi tiết giúp e từ câu 24 với ạ 

Những câu hỏi liên quan
Mọi người giúp e những câu e khoanh tròn với ạ. Mn ghi cách giải chi tiết nhất ý ạ.E cảm ơn ạ


40: Ta có: \(A=27x^3+8y^3-3x-2y\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)-\left(3x+2y\right)\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2-1\right)\)
Đúng 0
Bình luận (0)
Câu 21. Thực hiện thí nghiệm như hình vẽ dưới
Mọi người giúp e giải chi tiết với ạ
Mọi người giúp e giải chi tiết với ạ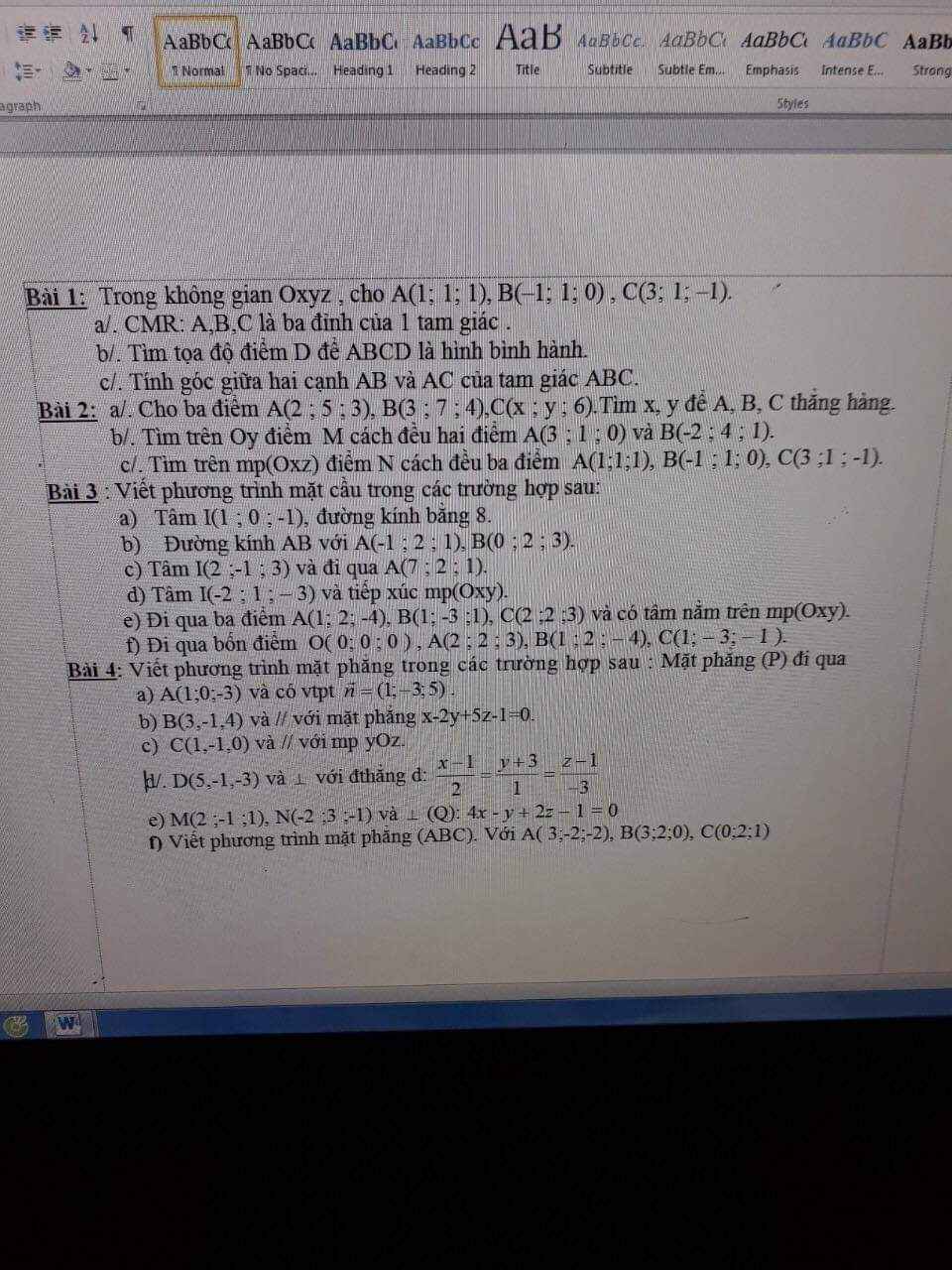
mọi người giúp mình giải chi tiết câu này với ạ
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x-2}+1}{\sqrt[]{x+3}-2}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x-2}+1\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)\left(\sqrt[]{x+3}+2\right)}{\left(\sqrt[]{x+3}-2\right)\left(\sqrt[]{x+3}+2\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(\sqrt[]{x+3}+2\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[]{x+3}+2}{\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1}\)
\(=\dfrac{\sqrt[]{1+3}+2}{\sqrt[3]{\left(1-2\right)^2}-\sqrt[3]{1-2}+1}=\dfrac{4}{3}\)
Đúng 1
Bình luận (1)
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
Đúng 0
Bình luận (0)
Mọi người giúp em giải chi tiết 2 câu này với ạ

mọi người giúp em giải chi tiết câu này với ạ 😿
theo mình thì câu trên: dưới mẫu trong căn bỏ n^2 ra làm nhân tử chung xong đặt nhân tử chung của cả mẫu là n^2 . câu dưới thì mình k biết!!
Đúng 0
Bình luận (0)
\(\lim\dfrac{-3n+2}{n-\sqrt{4n+n^2}}=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{\left(n-\sqrt{4n+n^2}\right)\left(n+\sqrt{4n+n^2}\right)}\)
\(=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{-4n}=\lim\dfrac{n\left(-3+\dfrac{2}{n}\right)n\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4n}\)
\(=\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}\)
Do \(\lim\left(n\right)=+\infty\)
\(\lim\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=\dfrac{\left(-3+0\right)\left(1+\sqrt{0+1}\right)}{-4}=\dfrac{3}{2}>0\)
\(\Rightarrow\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=+\infty\)
Đúng 0
Bình luận (0)
\(\lim\left(\sqrt[3]{n^3+9n^2}-n\right)=\lim\dfrac{\left(\sqrt[3]{n^3+9n^2}-n\right)\left(\sqrt[3]{\left(n^3+9n^2\right)^2}+n\sqrt[3]{n^3+9n^2}+n^2\right)}{\sqrt[3]{\left(n^3+9n^2\right)}+n\sqrt[3]{n^3+9n^2}+n^2}\)
\(=\lim\dfrac{9n^2}{\sqrt[3]{\left(n^3+9n^2\right)^2}+n\sqrt[3]{n^3+9n^2}+n^2}\)
\(=\lim\dfrac{9n^2}{n^2\sqrt[3]{\left(1+\dfrac{9}{n}\right)^2}+n^2\sqrt[3]{1+\dfrac{9}{n}}+n^2}\)
\(=\lim\dfrac{9}{\sqrt[3]{\left(1+\dfrac{9}{n}\right)^2}+\sqrt[3]{1+\dfrac{9}{n}}+1}\)
\(=\dfrac{9}{\sqrt[3]{\left(1+0\right)^2}+\sqrt[3]{1+0}+1}=\dfrac{9}{3}=3\)
Đúng 0
Bình luận (0)
mọi người giúp em câu nàu với ạ , giải chi tiết ạ
em cảm ơn nhiều
mọi người giúp mình giải chi tiết câu này với ạ😿😿
\(\lim\dfrac{3^n+2.6^n}{6^{n-1}+5.4^n}=\lim\dfrac{6^n\left[\left(\dfrac{3}{6}\right)^n+2\right]}{6^n\left[\dfrac{1}{6}+5\left(\dfrac{4}{6}\right)^n\right]}=\lim\dfrac{\left(\dfrac{3}{6}\right)^n+2}{\dfrac{1}{6}+5\left(\dfrac{4}{6}\right)^n}=\dfrac{0+2}{\dfrac{1}{6}+0}=12\)
\(\lim\left(\sqrt{n^2+9}-n\right)=\lim\dfrac{\left(\sqrt{n^2+9}-n\right)\left(\sqrt{n^2+9}+n\right)}{\sqrt{n^2+9}+n}=\lim\dfrac{9}{\sqrt{n^2+9}+n}\)
\(=\lim\dfrac{n\left(\dfrac{9}{n}\right)}{n\left(\sqrt{1+\dfrac{9}{n^2}}+1\right)}=\lim\dfrac{\dfrac{9}{n}}{\sqrt{1+\dfrac{9}{n^2}}+1}=\dfrac{0}{1+1}=0\)
\(\lim\dfrac{\sqrt{15+9n^2}-3}{5-n}=\lim\dfrac{n\sqrt{\dfrac{15}{n^2}+9}-3}{5-n}=\lim\dfrac{n\left(\sqrt{\dfrac{15}{n^2}+9}-\dfrac{3}{n}\right)}{n\left(\dfrac{5}{n}-1\right)}\)
\(=\lim\dfrac{\sqrt{\dfrac{15}{n^2}+9}-\dfrac{3}{n}}{\dfrac{5}{n}-1}=\dfrac{\sqrt{9}-0}{0-1}=-3\)
Đúng 1
Bình luận (1)










