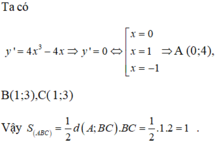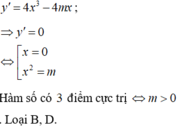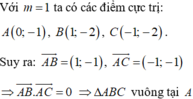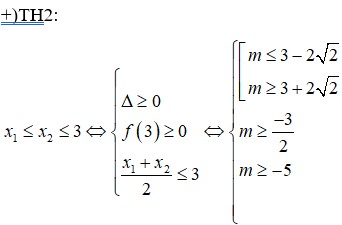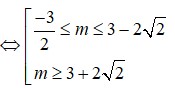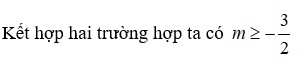Tìm cực trị của hàm số y=x⁴-2x²+5. Hàm số có 3 cực trị A,B,C tính chu vi của tam giác ABC

Những câu hỏi liên quan
Y=x^4-2(m+1)x^2+m^2 a)tìm m để hàm số có 3 cực trị tạo thành 1 tam giác nhận gốc toạ độ o là trọng tâm b)tìm m để hàm số có 3 cực trị tạo thành 3 đỉnh tam giác đều c)tìm m để hàm số có 3 cực trị tạo thành tam giác có bán kính đường tròn ngoại tiếp bằng 1 d) tìm m để hàm số có 3 cực trị và khoảng cách giữa 2 điểm cực tiểu là 5
Tìm cực trị của hàm số y=x³-3x+9. Hàm số có 2 cực trị A,B. Tính AB
Cho hàm số
y
x
4
-
2
x
2
+
4
. Gọi A,B,C là ba điểm cực trị của đồ thị hàm số. Tính diện tích S của tam giác ABC A. 4. B. 2. C. 10. D. 1.
Đọc tiếp
Cho hàm số y = x 4 - 2 x 2 + 4 . Gọi A,B,C là ba điểm cực trị của đồ thị hàm số. Tính diện tích S của tam giác ABC
A. 4.
B. 2.
C. 10.
D. 1.
Cho hàm số
y
x
4
-
2
m
x
2
+
m
2
-
2
. Tìm m để hàm số có 3 điểm cực trị và các điểm cực trị của đồ thị hàm số là ba đỉnh của một tam giác vuông? A. m 1 B. m ...
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 + m 2 - 2 . Tìm m để hàm số có 3 điểm cực trị và các điểm cực trị của đồ thị hàm số là ba đỉnh của một tam giác vuông?
A. m = 1
B. m = - 1
C. m = 2
D. m = - 2
Cho hàm số \(y=x^4-2m\left(m+1\right)x^2+m^2\) với m là tham số thực.
a) Tìm m để đồ thị hàm số trên có 3 cực trị tạo thành 3 đỉnh của tâm giác vuông
b) Tìm m để đồ thị hàm số trên có 3 cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho y = x3-3mx+1 có điểm A (2;3). Tìm m để hàm số có hai cực trị B,C sao cho tam giác ABC cân tại A
ta co y'=3x2-3m. h/s co 2 diem cuc tri<=>y'=0 co 2no pbiet # 2 <=>Δ>0 g(2)#0 <=>-4.3.(-3m)>0 3.(-2)2-3m#0 <=>m>0 m#4 ' ▲y'=0 =>x1=can(m) hoac x2=-can(m) (*) goi B(x1,x13-3mx1+1) va C(x2,x23-3mx2+1) thay (*) vao toa do B,C tinh vecto AB va vecto AC Cho 2 vecto dok =nhau binh phuong 2 ve => giai ra m. ket hop voi dk phia tren roi ket luan
Đúng 0
Bình luận (0)
cho hàm số y= 1/2x^2 có đồ thị (P) và đương thẳng (d) :y= 2x-3/2 a) tìm tọa độ điểm A và B của (d) và (P). tính chu vi tam giác AOB b) tìm tọa độ điểm C thuộc ox để chu vi tam giác ABC đạt giá trị nhỏ nhất Mọi người ơi giúp mìnhi với nha cảm ơn mọi người
Cho hàm số
y
x
4
-
2
m
2
x
2
+
1
(1). Các giá trị m để đồ thị hàm số (1) có 3 điểm cực trị A, B, C và diện tích tam giác ABC bằng 1 A.
±
2
B.
m
1
,
m
3
C.
m
±
1
D. ...
Đọc tiếp
Cho hàm số y = x 4 - 2 m 2 x 2 + 1 (1). Các giá trị m để đồ thị hàm số (1) có 3 điểm cực trị A, B, C và diện tích tam giác ABC bằng 1
A. ± 2
B. m = 1 , m = 3
C. m = ± 1
D. Đ á p á n k h á c
Gọi S là tập hợp các giá trị của tham số a để đồ thị hàm số
y
x
4
-
2
a
2
-
2
a
-
3
2
x
2
+
1
có ba điểm cực trị và ba điểm cực trị đó tạo thành một tam giác có chu...
Đọc tiếp
Gọi S là tập hợp các giá trị của tham số a để đồ thị hàm số y = x 4 - 2 a 2 - 2 a - 3 2 x 2 + 1 có ba điểm cực trị và ba điểm cực trị đó tạo thành một tam giác có chu vi bằng 2 2 + 2 . Số tập hợp con của tập hợp S là
A. 2
B. 8
C. 16
D. 4
Chọn đáp án C.
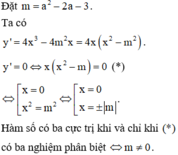
Tọa độ các điểm cực trị của đồ thị hàm số là

Đúng 0
Bình luận (0)