Tìm nghiệm:
x2+5x
x2-6x
3x2-5x-8
4x3+2x2-6x
C/m vô nghiệm :
x2+2x+7
Bài 19 trang 7 SBT Toán 8 Tập 1: Tìm giá trị nhỏ nhất của các đa thức:
a. P = x2 – 2x + 5
b. Q = 2x2 – 6x
c. M = x2 + y2 – x + 6y + 10
\(a,P=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=1\)
\(b,Q=2x^2-6x=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}\right)=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(c,M=\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
a: Ta có: \(P=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
Bài 8*: Tìm giá trị nhỏ nhất của biểu thức a) P= x2 + 10x + 27
b) Q=2x2 - 6x
c) M= x2 + y2 - x + 6y + 10
a: ta có: \(P=x^2+10x+27\)
\(=x^2+10x+25+2\)
\(=\left(x+5\right)^2+2\ge2\forall x\)
Dấu '=' xảy ra khi x=-5
c,|x2 -3x|=5x
c,|x2 +5x|=6x
c,|x2 +2x|=-x
c: |x^2-3x|=5x
=>(x^2-3x)^2=(5x)^2 và x>=0
=>(x^2-3x-5x)(x^2-3x+5x)=0 và x>=0
=>x^2(x-8)(x+2)=0
=>x=0 và x=8
c: |x^2+5x|=6x
=>(x^2+5x)^2=(6x)^2 và x>=0
=>(x^2+5x-6x)(x^2+5x+6x)=0 và x>=0
=>x^2(x-1)(x+11)=0 và x>=0
=>x=0 hoặc x=1
c: |x^2+2x|=-x
=>(x^2+2x)^2=(-x)^2 và x<=0
=>(x^2+2x+x)(x^2+2x-x)=0 và x<=0
=>(x^2+x)(x^2+3x)=0 và x<=0
=>\(x\in\left\{0;-1;-3\right\}\)
\(\left|x^2-3x\right|=5x\\ \Leftrightarrow\left[{}\begin{matrix}x^2-3x=5x\\x^2-3x=-5x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2-8x=0\\x^2+2x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\left(x-8\right)=0\\x\left(x+2\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=8\\x=-2\end{matrix}\right.\)
\(\left|x^2+5x\right|=6x\\ \Leftrightarrow\left[{}\begin{matrix}x^2+5x=6x\\x^2+5x=-6x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2-x=0\\x^2+11x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\left(x-1\right)=0\\x\left(x+11\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-11\end{matrix}\right.\)
\(\left|x^2+2x\right|=-x\\ \Leftrightarrow\left[{}\begin{matrix}x^2+2x=-x\\x^2+2x=x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2+3x=0\\x^2+x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\left(x+3\right)=0\\x\left(x+1\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-3\\x=-1\end{matrix}\right.\)
\(c1:\left|x^2-3x\right|=5x\)
Th1:x=0 \(=>\left|x^2-3x\right|=5x\)
\(=>\left|0^2-3.0\right|=5.0\)
\(=>0=0\)
\(=>x=0\) thỏa mãn
Th2:x>0 \(=>\left[{}\begin{matrix}x^2-3x=5x\\x^2-3x=-5x\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x^2=8x\\x^2=-2x\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
\(=>x\in\left\{-2;8\right\}\)
\(c2,\left|x^2+5x\right|=6x\)
\(=>\left[{}\begin{matrix}x^2+5x=6x\\x^2+5x=-6x\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x^2=x\\x^2=-11x\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x^2-x=0\\x=-11\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x\left(x-1\right)=0\\x=-11\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x=0\\x-1=0\\x=-11\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x=0\\x=1\\x=-11\end{matrix}\right.\)
\(=>x\in\left\{0;1;-11\right\}\)
\(c3,\left|x^2+2x\right|=-x\)
Loại vì GTTĐ luôn luôn ≥ 0
Tìm điều kiện của tham số m để phương trình 2 x 2 + 5 x + m − 1 = 0 vô nghiệm
A. m > 8 33
B. Không tồn tại m
C. m > 33 8
D. m < 33 8
Phương trình 2x2 + 5x + m − 1 = 0 (a = 2; b = 5; c = m – 1)
⇒ ∆ = 52 – 4.2.(m – 1) = 25 – 8m + 8 = 33 – 8m
Để phương trình đã cho vô nghiệm thì
a ≠ 0 Δ < 0 ⇔ 2 ≠ 0 ( l d ) 33 − 8 m < 0 ⇔ m > 33 8
Vậy với m > 33 8 thì phương trình vô nghiệm.
Đáp án cần chọn là: D
Bài 5: Tìm nghiệm của các đa thức sau: Dạng 1: a) 4x + 9 b) -5x + 6 c) 7 – 2x d) 2x + 5 Dạng 2: a) ( x+ 5 ) ( x – 3) b) ( 2x – 6) ( x – 3) c) ( x – 2) ( 4x + 10 ) Dạng 3: a) x2 -2x b) x2 – 3x c) 3x2 – 4x d) ( 2x- 1)2 Dạng 4: a) x2 – 1 b) x2 – 9 c)– x 2 + 25 d) x2 - 2 e) 4x2 + 5 f) –x 2 – 16 g) - 4x4 – 25 Dạng 5: a) 2x2 – 5x + 3 b) 4x2 + 6x – 1 c) 2x2 + x – 1 d) 3x2 + 2x – 1
1. Cho f(x)= x3 - 2x2 + 3x + 1; g(x)+ x3 + x - 1; h(x)= 2x2 -1
a) Tính f(x) - g(x) + h(x)
b) Tìm x sao cho f(x) - g(x) + h(x) = 0
2. Tìm nghiệm của
a) 5x + 3 (3x + 7) - 35
b) x2 + 8x - (x2 + 7x + 8) - 9
3. Tìm f(x) = x3 + 4x2 - 3x + 2; g(x) = x2 (x+4) + x - 5
Tìm x sao cho f(x) = g(x)
4. Tìm m sao cho k(x)= mx2 - 2x + 4 có nghiệm là -2
Cho phương trình: x2 - 5x + m - 1 = 0 (*). Tìm m để phương trình (*) có 2 nghiệm phân biệt x1;x2 sao cho: 2x2 = \(\sqrt{x_1}\)
\(\Delta=\left(-5\right)^2-4\left(m-1\right)\)
\(=25-4m+4\)
\(=29-4m\)
Để pt có 2 nghiệm thì \(\Delta>0\)
\(\Leftrightarrow m< \dfrac{29}{4}\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m-1\end{matrix}\right.\) (1)
\(2x_2=\sqrt{x_1}\) ; \(ĐK:x_1;x_2\ge0\)
\(\Leftrightarrow4x_2^2=\left|x_1\right|\)
\(\Leftrightarrow4x_2^2=x_1\) (2)
Thế \(x_1=4x^2_2\) vào \(\left(1\right)\), ta được:
\(\left\{{}\begin{matrix}4x_2^2+x_2-5=0\\4x_2^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x_2=-\dfrac{5}{4}\left(ktm\right)\\x_2=1\left(tm\right)\end{matrix}\right.\\4.1^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=1\\m=5\end{matrix}\right.\)
\(\left(2\right)\Rightarrow x_1=4\)
Vậy \(\left\{{}\begin{matrix}m=5\\x_1=4\\x_2=1\end{matrix}\right.\)
Tìm giá trị nhỏ nhất của biểu thức:
1. x2-2x-5
2. 3x2+5x-2
3. 2x2-7x+7
1: Ta có: \(x^2-2x-5\)
\(=x^2-2x+1-6\)
\(=\left(x-1\right)^2-6\ge-6\forall x\)
Dấu '=' xảy ra khi x=1
2: ta có: \(3x^2+5x-2\)
\(=3\left(x^2+\dfrac{5}{3}x-\dfrac{2}{3}\right)\)
\(=3\left(x^2+2\cdot x\cdot\dfrac{5}{6}+\dfrac{25}{36}-\dfrac{49}{36}\right)\)
\(=3\left(x+\dfrac{5}{6}\right)^2-\dfrac{49}{12}\ge-\dfrac{49}{12}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{5}{6}\)
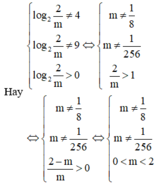
Cho phương trình m . 2 x 2 - 5 x + 6 + 2 1 - x 2 = 2 . 2 6 - 5 x + m . Tìm tất cả các giá trị thực của tham số m để phương trình có 4 nghiệm phân biệt
![]()
![]()
Cho phương trình m . 2 x 2 - 5 x + 6 + 2 1 - x 2 = 2 . 2 6 - 5 x . Tìm tất cả các giá trị thực của tham số m để phương trình có 4 nghiệm phân biệt.
A. m ∈ 0 ; 2
B. m ∈ 0 ; + ∞
C. m ∈ 0 ; 2 \ 1 8 ; 1 256
D. m ∈ - ∞ ; 2 \ 1 8 ; 1 256
Chọn C.
Phương pháp: Biến đổi đưa về phương trình tích.
Cách giải:
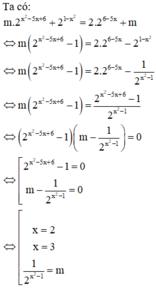
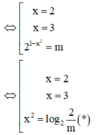
Vậy để phương trình đã cho có 4 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt khác 2 và 3.