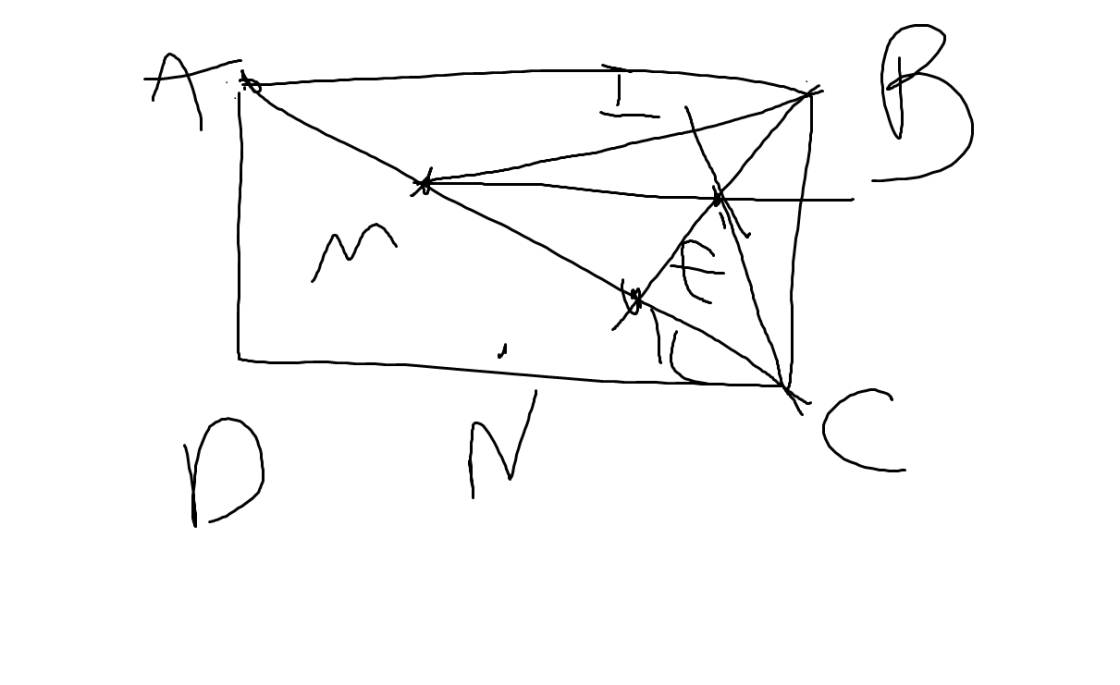
vẽ hình giúp với.
cho hình chữ nhật abcd.kẻ bk vuông với ac ở k. gọi m và n là trung điểm ak và cd.kẻ ci vuông với bm ở i và cắt bk ở e.
1)chứng minh ME//NC//AB và E là trung điểm KB.
2)tứ giác MNCE là hình gì?
3)chứng minh BM vuông góc MN.
4)cho bk =4cm,ac=10cm.tính diện tích ABCD