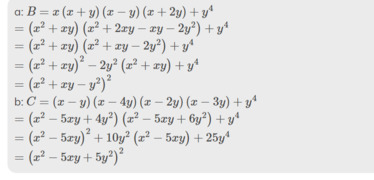với x y thuộc z , cm đa thức sau là số lập phương (x+y)(x+2y)(x+3y)(x+4y)+y4

Những câu hỏi liên quan
Bài 1: Cmr các số sau đây là số chính phương với x,y thuộc Z
a) B= x.(x-y) . ( x+y) . ( x+2y) + y4
b) C= ( x-y). ( x-2y) . ( x-3y) . ( x-4y) + y4
Bài 1: Cmr các số sau đây là số chính phương với x,y thuộc Z
a) B= x.(x-y) . ( x+y) . ( x+2y) + y4
b) C= ( x-y). ( x-2y) . ( x-3y) . ( x-4y) + y4
a: \(B=x\left(x+y\right)\left(x-y\right)\left(x+2y\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+2xy-xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)^2-2y^2\left(x^2+xy\right)+y^4\)
\(=\left(x^2+xy-y^2\right)^2\)
b: \(C=\left(x-y\right)\left(x-4y\right)\left(x-2y\right)\left(x-3y\right)+y^4\)
\(=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(=\left(x^2-5xy\right)^2+10y^2\left(x^2-5xy\right)+25y^4\)
\(=\left(x^2-5xy+5y^2\right)^2\)
Đúng 0
Bình luận (0)
Cho x, y thuộc Z. Chứng minh các biểu thức sau là số chính phương
A=x(x-y)(x+y)(x+2y)+y4
B=(x+1)(x+3)(x+4)(x+6)+9
C=(x-y)(x-2y)(x-3y)(x-4y)+y^4
a)CMR với mọi x,y thuộc Z thì
S=(x+y)(x+2y)(x+3y)(x+4y)y^4 là số chính phương
b) Cho T=(t-1)(t-3)(t-4)(t-6)+9
1)CM: T lớn hơn hoặc bằng 0 với mọi t
2)T là số chính phương với mọi t thuộc Z
Cho x,y thuộc Z,chứng minh rằng các số sau là số chính phương:
M=(x+1)(x+3)(x+4)(x+6)+9
N=(x-y)(x-2y)(x-3y)(x-4y)+y^4
=[(x+1)(x+6)][(x+3)(x+4)]+9
Sau khi nhân thì sẽ có kết quả sau : =(x2+7x+6)(x2+7x+12)+9 . Sẽ đặt ẩn phụ là (x2+7x+6) = a . suy ra a2+6a+9=(x+3)2 rồi lại thay ngược lại thì có kết quả cuối cùng là (x2+7x+9)2=>M là số chính phương
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số nguyên của x,y thì giá trị của đa thức
P= (x+y)(x+2y)(x+3y)(x+4y)+y^4 là một số chính phương
A=(x+y)(x+2y)(x+3y)(x+4y)+y4
=[(x+y)(x+4y)] [(x+2y)(x+3y)]+y4
=(x2+5xy+4y2) (x2+5xy+6y2)+y4
Gọi x2+5xy+4y2=a
\(\Rightarrow\)a(a+2y2)+y4
=a2+2ay2+y4
=(y2)2+2ay2+a2
=(a+y2)2
=(x2+5xy+4y2+y2)2
=(x2+5xy+5y2)2 là SCP
Phân tích đa thức thành nhân tử : (x + y)(x + 2y)(x + 3y)(x + 4y) + y4
\(\left(x+y\right)\left(x+2y\right)\left(x+3y\right)\left(x+4y\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+6y^2\right)+y^4\)
\(=\left(x^2+5xy\right)^2+10y^2\left(x^2+5xy\right)+24y^4+y^4\)
\(=\left(x^2+5xy+5y^2\right)^2\)
Đúng 1
Bình luận (0)
Bài 1: Phân tích đa thức sau :
a)2x(xy+y^2-3)
b)(x-y)(2x+y)
c)(x-2y)^2
d)(2x-y)(y+2x)
bài 2: Phân tích các đơn thức thành nhân tử
a)3x^2-3xy
b)x^2-4y^2
c)3x-3y+xy-y^2
d)x^2-1+2y-y^2
Bài 3: Tìm x biết:
a)3x^2-6x=0
b)Tìm x,y thuộc z biết: x^2+4y^2-2xy=4
Bài 2:
a: \(3x^2-3xy=3x\left(x-y\right)\)
b: \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
c: \(3x-3y+xy-y^2=\left(x-y\right)\left(3+y\right)\)
d: \(x^2-y^2+2y-1=\left(x-y+1\right)\left(x+y-1\right)\)
Đúng 2
Bình luận (0)
cho x,y thuộc z cm a=(x-y)(x-2y(x-3y)(x-4y)+y^4
CM a là số chính phương, đề như thế này
Ta có:
\(a=\left(x-y\right)\left(x-2y\right)\left(x-3y\right)\left(x-4y\right)+y^4\)
\(a=\left[\left(x-y\right)\left(x-4y\right)\right]\left[\left(x-2y\right)\left(x-3y\right)\right]+y^4\)
\(a=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(a=\left[\left(x^2-5xy+5y^2\right)-y^2\right]\left[\left(x^2-5xy+5y^2\right)+y^2\right]+y^4\)
\(a=\left(x^2-5xy+5y^2\right)^2-y^4+y^4\)
\(a=\left(x^2-5xy+5y^2\right)^2\) là SCP
=>đpcm
Chứng minh là một SCP chứ gì (:
A = ( x - y )( x - 2y )( x - 3y )( x - 4y ) + y4
= [ ( x - y )( x - 4y ) ][ ( x - 2y )( x - 3y ) ] + y4
= ( x2 - 5xy + 4y2 )( x2 - 5xy + 6y2 ) + y4 (1)
Đặt t = x2 - 5xy + 5y2
(1) <=> ( t - y2 )( t + y2 ) + y4
= t2 - y4 + y4
= t2 = ( x2 - 5xy + 5y2 )2
Vì x, y ∈ Z => x2 ∈ Z , -5xy ∈ Z , 5y2 ∈ Z
=> ( x2 - 5xy + 5y2 )2 là một SCP
=> đpcm