- Xét phương trình hoành độ giao điểm :\(x^2-2x+2=x+m\)

\(\Leftrightarrow x^2-3x+2-m=0\)

Có \(\Delta=b^2-4ac=9-4\left(2-m\right)=9-8+4m=4m+1\)

- Để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta>0\) \(\Leftrightarrow m>-\dfrac{1}{4}\left(1\right)\)

Theo viet : \(\left\{{}\begin{matrix}x_a+x_b=3\\x_ax_b=2-m\end{matrix}\right.\)

- Ta có : \(OA^2+OB^2=10\)

\(\Leftrightarrow x^2_A+y^2_A+x_B^2+y^2_B=10\)

\(\Leftrightarrow x^2_a+x^2_b+\left(x_a+m\right)^2+\left(x_b+m\right)^2=10\)

\(\Leftrightarrow2x^2_a+2x^2_b+2m\left(x_a+x_b\right)+2m^2=10\)

\(\Leftrightarrow2\left(x_a+x_b\right)^2-4x_ax_b+2m\left(x_a+x_b\right)+2m^2-10=0\)

\(\Leftrightarrow18-4\left(2-m\right)+6m+2m^2-10=0\)

\(\Leftrightarrow2m^2+10m=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-5\end{matrix}\right.\)

- Kết hợp ĐK (1) => m = 0 ( TM )

Vậy ...

Phương trình hoành độ giao điểm của (C) và d là:

x + 1 x - 1 = 2 x + m ⇔ x ≠ 1 f x = 2 x 2 + m - 3 - m - 1

Ta có

∆ = m 2 + 2 m + 7 > 0 ∀ m f 1 = - 2 ≠ 0

=> d luôn cắt tại hai điểm phân biệt A, B.

Gọi x 1 ; x 2 lần lượt là hoành độ các điểm A, B. Khi đó A O B ⏞ nhọn.

⇔ cos A O B ⏞ = O A 2 + O B 2 - A B 2 2 . O A . O B > 0 ⇔ O A 2 + O B 2 > A B 2 ⇔ x 1 2 + 2 x 1 + m 2 + x 2 2 + 2 x 2 + m 2 > 5 x 2 - x 1 2

Sử dụng định lí Viet và giải bất phương trình theo m ta thu được m > 5

Đáp án C

Phương trình hoành độ giao điểm:  x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0

(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4

Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2

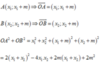
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4

Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2  khi m = − 5 2

Đáp án cần chọn là: A

Phương trình hoành độ giao điểm: x2−(1−2m)x+m2=0x2−(1−2m)x+m2=0

Δ=(1−2m)2−4m2=−4m+1>0⇒m>14Δ=(1−2m)2−4m2=−4m+1>0⇒m>14

Do x1x1 là nghiệm của pt nên

x21−(1−2m)x1+m2⇔x21=(1−2m)x1−m2x12−(1−2m)x1+m2⇔x12=(1−2m)x1−m2

Thế vào bài toán:

⇔((1−2m)x1−m2−x1)(2mx2+m2)+m4+5m=3⇔((1−2m)x1−m2−x1)(2mx2+m2)+m4+5m=3

⇔−(2mx1+m2)(2mx2+m2)+m4+5m−3=0⇔−(2mx1+m2)(2mx2+m2)+m4+5m−3=0

⇔−4m2x1x2−2m3(x1+x2)−m4+m4+5m−3=0⇔−4m2x1x2−2m3(x1+x2)−m4+m4+5m−3=0

⇔−4m2.m2−2m3(1−2m)+5m−3=0⇔−4m2.m2−2m3(1−2m)+5m−3=0

⇔2m3−5m+3=0⇔2m3−5m+3=0

⇔(m−1)(2m2+2m−3)=0⇒⎡⎣⎢⎢⎢m=1m=−1+7√2m=−1−7√2<14(l)

Phương trình hoành độ giao điểm: x2−(1−2m)x+m2=0x2−(1−2m)x+m2=0

Δ=(1−2m)2−4m2=−4m+1>0⇒m>14Δ=(1−2m)2−4m2=−4m+1>0⇒m>14

Do x1x1 là nghiệm của pt nên

x21−(1−2m)x1+m2⇔x21=(1−2m)x1−m2x12−(1−2m)x1+m2⇔x12=(1−2m)x1−m2

Thế vào bài toán:

⇔((1−2m)x1−m2−x1)(2mx2+m2)+m4+5m=3⇔((1−2m)x1−m2−x1)(2mx2+m2)+m4+5m=3

⇔−(2mx1+m2)(2mx2+m2)+m4+5m−3=0⇔−(2mx1+m2)(2mx2+m2)+m4+5m−3=0

⇔−4m2x1x2−2m3(x1+x2)−m4+m4+5m−3=0⇔−4m2x1x2−2m3(x1+x2)−m4+m4+5m−3=0

⇔−4m2.m2−2m3(1−2m)+5m−3=0⇔−4m2.m2−2m3(1−2m)+5m−3=0

⇔2m3−5m+3=0⇔2m3−5m+3=0

⇔(m−1)(2m2+2m−3)=0⇒ m=1 hoặc m=−1+7√2  hoặc m=−1−7√2<14(l)

Vậy ............................................

  k cho mk nha !!!

có đáp án chưa ạ ?