Cho tứ giác ABCD , Gọi E,F,I theo thứ tự là trung điểm của AD,BC,AC . Chứng minh EI // CD, IF// AB

Những câu hỏi liên quan
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng:
a) EI//CD, IF//AB.
b)EF=<AB+CD/2
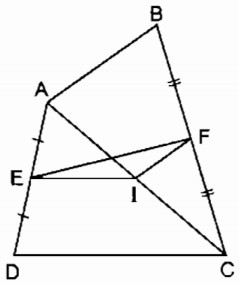
a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Và EI=CD/2
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
Và IF=AB/2
b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)
Mà EI=\(\dfrac{CD}{2}\); IF=\(\dfrac{AB}{2}\) (chứng minh trên) ⇒EF≤\(\dfrac{CD}{2}+\dfrac{AB}{2}\)
Vậy EF≤\(\dfrac{AB+CD}{2}\) (dấu bằng xảy ra khi AB // CD)
Tick nha 😘
Đúng 4
Bình luận (0)
a) Xét ΔACD có
I là trung điểm của AC
E là trung điểm của AD
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔABC có
I là trung điểm của AC
F là trung điểm của BC
Do đó: IF là đường trung bình của ΔABC
Suy ra: IF//AB
Đúng 2
Bình luận (0)
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung đếm của AD, BC, AC. Chứng minh rằng: EI//CD, IF//AB
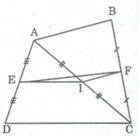
* Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ADC
⇒EI // CD (tỉnh chất đường trung bình của tam giác) và EI = CD / 2
* Trong tam giác ABC, ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒IF // AB (tỉnh chất đường trung bình của tam giác) và IF= AB / 2
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng:
a) EI//CD, IF//AB.
b) ![]()
a: Xét ΔADC có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình
=>EI//CD
Xét ΔCAB có
F là trung điểm của BC
I là trung điểm của AC
Do đó: FI là đường trung bình
=>FI//AB
Đúng 0
Bình luận (1)
cho tứ giác ABCD. Gọi E,F,I thheo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng
a) Ei//CD, IF//AB
a) Tam giác ACD có:
E là trung điểm của AD
I là trung điểm của AC
=> EI là ĐTB của tam giác ACD
=> EI // CD
Chứng minh tương tự IF là ĐTB của tam giác ABC
=> IF//AB
Đúng 1
Bình luận (0)
Bài 2.Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung đếm của AD, BC, AC. Chứng minh rằng:
a. EI//CD, IF//AB
b. ![]()
Cho tư sgiacs ABCD , Gọi E,F,I theo thứ tự là trung điểm của AD,BC,AC . Chứng minh EI // CD, IF// AB
Ta có : E là trung điểm của AD, I là trung điểm của AC .
=> EI là đường trung bình của tam giác ADC .
=> EI // DC
CMTT : Ta được : FI là đường trung bình của tam giác ABC
=> FI // AB
Đúng 1
Bình luận (0)
Tam giác ACD có:
E là trung điểm của AF
I là trung điểm của AC
=> IE là ĐTB của tam giác ACD
=> IE // CD
Tam giác ACB có:
F là trung điểm của BC
I là trung điểm của AC
=> IF là ĐTB của tam giác ACB
=> IF // AB
Đúng 0
Bình luận (1)
Tam giác ACB có:
F là trung điểm của BC
I là trung điểm của AC
=> IF là ĐTB của tam giác ACB
=> IF // AB
nha học tốt ![]()
![]()
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng :
a) EI // CD, IF // AB
b) \(EF\le\dfrac{AB+CD}{2}\)
Ta có hình vẽ:
a) Xét \(\Delta ADC\) có:
AE = ED (gt)
AI = IC (gt)
=> EI là đường trung bình
=> EI // DC
Xét \(\Delta CAB\) có:
AI = IC (gt)
BF = FC (gt)
=> IF là đường trung bình
=> IF // AB
b) Ta có: EF \(\le\) EI + IF
mà IF + EF = \(\dfrac{1}{2}\) AB + \(\dfrac{1}{2}\) CD
= \(\dfrac{1}{2}\) (AB + CD)
=> EF \(\le\) \(\dfrac{\left(AB+CD\right)}{2}\) (đpcm)
Đúng 0
Bình luận (0)
cho tứ giác ABCD .Gọi E;I;F theo thứ tự là trung điểm của AD ,BD ,BC.Chứng minh rằng :EI//AB; IF //CD
Áp dụng t/c đường trung bình của tam giác vào tam giác DAB có :
E trung điểm AD ; I trung điểm BD
=> EI // AB.
Áp dụng t/c đường trung bình của tam giác vào tam giác DBC có :
F trung điểm BC ; I trung điểm BD
=> IF // DC
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng:
a) EI // CD, IF // AB
b) EF < \(\frac{AB+CD}{2}\)
Giúp mình với nhé, thanks nhìu























