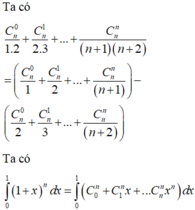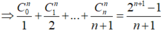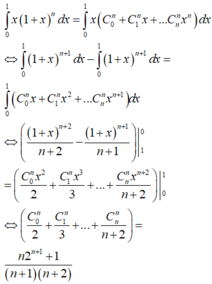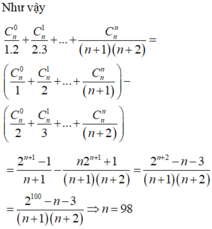Tìm tất cả các số tự nhiên n thỏa mãn bất phương trình: 2(n-1)-5(n-2>0.

Những câu hỏi liên quan
Tìm số tự nhiên n thỏa mãn cho bất phương trình sau 2(n-2)-5(n+1)>0
`2 ( n - 2 ) - 5 ( n + 1 ) > 0`
`<=> 2x - 4 - 5n - 5 > 0`
`<=> -3n > 9`
`<=> n < 3`
Mà `n in NN`
`=> n = { 0 ; 1 ; 2 }`
Vậy `n = { 0 ; 1 ; 2 }`
Đúng 3
Bình luận (0)
2(n−2)−5(n+1)>0
=>2x−4−5n−5>0
=>−3n>9
=>n<3
Mà n∈N
⇒n={0;1;2}
KL:...
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số tự nhiên (n;z) thỏa mãn phương trình: \(2^n+12^2=z^2-3^2\)
Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau: 3(5 – 4n) + (27 + 2n) > 0
Ta có: 3(5 – 4n) + (27 + 2n) > 0
⇔ 15 – 12n + 27 + 2n > 0
⇔ -10n + 42 > 0
⇔ -10n > -42
⇔ n < 4,2
Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4.
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số tự nhiên (n,z) thỏa mãn phương trình :
\(2^n+12^2=z^2-3^2\)
Nếu n lẻ thì \(2^n\equiv-1\left(mod3\right)\)
Từ pt đã cho ta suy ra
\(z^2\equiv-1\left(mod3\right)\) (loại)
Nếu n chẵn thì \(n=2m\left(m\in N\right)\)và pt đã cho trở thành:
\(z^2-2^{2m}=153\) hay \(\left(z-2^m\right)\left(z+2^m\right)=153\)
Cho \(z+2^m\)và\(z-2^m\)là các ước của 153 ta tìm được z=13;m=2=>n=4
Vậy n=4;z=13
Đúng 0
Bình luận (0)
C
n
0
1.2
+
C
n
1
2.3
+
C
n
2
3.4
+
...
+
C
n
n
n
+
1...
Đọc tiếp
C
n
0
1.2
+
C
n
1
2.3
+
C
n
2
3.4
+
...
+
C
n
n
n
+
1
n
+
2
=
2
100
−
n
−
3
n
+
1
n
+
2
Tìm tất cả số tự nhiên n thỏa mãn phương trình trên.
A. n = 100
B. n = 98
C. n = 99
D. n = 101
Bài 1:a) Tìm các số tự nhiên n thỏa mãn bất phương trình:(n + 2)2 - (x - 3) (n + 3) le40b) Tìm các số tự nhiên n thỏa mãn đồng thời cả hai bất phương trình sau:4 (n + 1) + 3n - 6 19 và (n - 3)2 - (n + 4) (n - 4) le43Bài 2:Chứng minh bất đẳng thức sauAleft(a+bright)left(frac{1}{a}+frac{1}{b}right)ge4 Bfrac{a+b}{c}+frac{b+c}{a}+frac{c+a}{b}ge6;left(a,b,c0right)
Đọc tiếp
Bài 1:
a) Tìm các số tự nhiên n thỏa mãn bất phương trình:
(n + 2)2 - (x - 3) (n + 3) \(\le\)40
b) Tìm các số tự nhiên n thỏa mãn đồng thời cả hai bất phương trình sau:
4 (n + 1) + 3n - 6 < 19 và (n - 3)2 - (n + 4) (n - 4) \(\le43\)
Bài 2:
Chứng minh bất đẳng thức sau
\(A=\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)\ge4\) \(B=\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}\ge6;\left(a,b,c>0\right)\)
Bài 2:
A = (a+b)(1/a+1/b)
Có: \(a+b\ge2\sqrt{ab}\)
\(\frac{1}{a}+\frac{1}{b}\ge2\sqrt{\frac{1}{ab}}\)
=> \(\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)\ge2\sqrt{ab}.2\sqrt{\frac{1}{ab}}=4\)
=> ĐPCM
Đúng 0
Bình luận (0)
1.b)
Pt (1) : 4(n + 1) + 3n - 6 < 19
<=> 4n + 4 + 3n - 6 < 19
<=> 7n - 2 < 19
<=> 7n - 2 - 19 < 0
<=> 7n - 21 < 0
<=> n < 3
Pt (2) : (n - 3)^2 - (n + 4)(n - 4) ≤ 43
<=> n^2 - 6n + 9 - n^2 + 16 ≤ 43
<=> -6n + 25 ≤ 43
<=> -6n ≤ 18
<=> n ≥ -3
Vì n < 3 và n ≥ -3 => -3 ≤ n ≤ 3.
Vậy S = {x ∈ R ; -3 ≤ n ≤ 3}
Đúng 0
Bình luận (0)
tím các số tự nhiên n thỏa mãn mỗi bất phương trình sau:
a, 3(5-4n )+(27+2n)>0
b, (n+2)^2 - (n-3)(n+3)\(\le\) 40
Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau: n + 2 2 – (n – 3)(n + 3) ≤ 40
Ta có: n + 2 2 – (n – 3)(n + 3) ≤ 40
⇔ n 2 + 4n + 4 – n 2 + 9 ≤ 40
⇔ 4n < 40 – 13
⇔ n < 27/4
Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4; 5; 6.
Đúng 0
Bình luận (0)
1. Tìm tất cả các số tự nhiên n sao cho: P 1! + 2! + 3! + ... + n! là số chính phương2. Chứng minh rằng với n là số nguyên dương bất kì thì: A1+frac{1}{4}+frac{1}{3^2}+...+frac{1}{n^2} 1,653. Tìm tất cả các số tự nhiên không là tổng của 2 hợp số.4. Tìm các số nguyên x,y thỏa mãn : left(x+2003right)left(x+2005right).4^y3025
Đọc tiếp
1. Tìm tất cả các số tự nhiên n sao cho: P = 1! + 2! + 3! + ... + n! là số chính phương
2. Chứng minh rằng với n là số nguyên dương bất kì thì:
\(A=1+\frac{1}{4}+\frac{1}{3^2}+...+\frac{1}{n^2}< 1,65\)
3. Tìm tất cả các số tự nhiên không là tổng của 2 hợp số.
4. Tìm các số nguyên x,y thỏa mãn : \(\left(x+2003\right)\left(x+2005\right).4^y=3025\)