bạn tham khảo tại đây nhé, mk bận ko thể giải cho bn dc, thông cảm nha, h mk phải ik ăn đám cứ r, chúc bn hc tốt nhé

http://pitago.vn/question/a-dung-hinh-thang-abcd-ab-cd-biet-day-ab-2-cm-hai-10453.html

trên CD lấy điểm H sao cho DH=AB

Tứ giác ABHD có DH=AB và DH//AB

=>ABHD là HBH

=>AD=BH

DH+HC=CD

2+HC=5

=>HC=3

áp dụng BĐT tam giác trong tam giác BHC ta có

BH+BC>HC

hay AD+BC>3

me too

Đề sửa lại: Hình thang ABCD ( AB//CD ) có AB=2cm CD=5cm. Chứng minh rằng AD + BC>3cm

Giải:

Tg ADC có DC - AD < AC (bất đằng thức tam giác)(1)

tg ABC có AC < AB + BC (bất đằng thức tam giác)(2)

Từ (1) và (2) => DC - AD < AB + BC => DC - AB < AB + BC

mà AB=2cm CD=5cm => 5 - 2 < AB + BC hay AB + BC > 3 (đpcm)

Chúc bạn thành công!

Giải: (sửa giúp)

...v.v...

Từ (1) và (2) => DC - AD < AB + BC => DC - AB < AD + BC

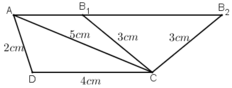
* Dựng hình:

   - Dựng tam giác ADC có AD = 2cm, DC = 4cm, CA = 5cm.

   - Dựng tia Ax song song với CD.

   - Đường tròn (C; 3cm) cắt Ax tại B1 và B2.

Hình thang ABCD với B ≡ B1 hoặc B ≡ B2 là hình thang cần dựng.

* Chứng minh

   + Tứ giác ABCD có AD = 2cm, DC = 4cm, CA = 5cm.

   + Ax // CD ⇒ AB // CD ⇒ ABCD là hình thang.

   + B ∈ (C; 3cm) ⇒ BC = 3cm.

từ A hạ \(AE\perp DC\)

từ B hạ \(BF\perp DC\)

\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật

\(=>AB=EF=2cm\)

vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)

mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)

\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)

xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)

\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)

hình như bạn cho cái đề thiếu BC nhỉ!

Chung minh ABD đồng dạng với BDC

=> \(\widehat{ABD}\)=\(\widehat{BDC}\)

hai góc này ở vị trí sole trong

=> AB//CD