Vẽ tam giác ABC biết Bˆ=90o, BC=2cm, Cˆ=60o Đo được độ dài cạnh AC là:

Những câu hỏi liên quan
Vẽ tam giác ABC biết ∠B =90o,∠C =60o, BC = 2cm. Sau đó đo AC để kiểm tra rằng AC = 4cm.
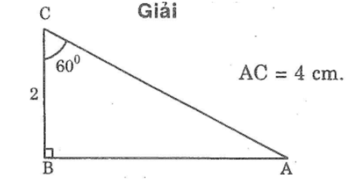
+ Vẽ tam giác ABC:
-) Vẽ đoạn thẳng BC = 2 cm.
-) Trên cùng một nửa mặt phăng bờ BC, vẽ các tia Bx và Cy sao cho ∠CBx = 90º và &BCy = 60º.
Hai tia trên cắt nhau tại A ta được tam giác ABC.
+) Đo AC ta được: AC = 4cm.
Đúng 0
Bình luận (0)
Vẽ tam giác ABC biết AC = 2cm, A ^ = 90 o , C ^ = 60 o
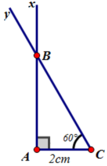
Cách vẽ:
- Vẽ đoạn thẳng AC = 2cm
- Trên cùng một nửa mặt phẳng bờ AC vẽ các tia Ax và Cy sao cho 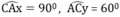
Hai tia cắt nhau tại B. Ta được tam giác ABC cần vẽ.
Đúng 0
Bình luận (0)
Cho tam giác ABC có Aˆ=60o,Bˆ=105o. So sánh độ dài ba cạnh của △ABC
Cho tam giác ABC có Aˆ=90o,Bˆ=60o. Kẻ AH vuông góc với BC (H ∈ BC)
So sánh HACˆ và ABCˆ
Xét tam giác ABC vuông tại A
Ta có \(\widehat{BAC}=90^o\)(GT)
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=90^o\)( hai góc bù nhau )
Mà \(\widehat{ABC}=60^o\)(GT)
\(\Rightarrow\widehat{ACB}=30^o\)( Bù nhau )
Xét tam giác AHC vuông tại H ta có :
\(\widehat{ACH}=30^o\)(CMT)
\(\Rightarrow\widehat{ACH}+\widehat{HAC}=90^o\)( hai góc bù nhau )
\(\Rightarrow30^o+\widehat{HAC}=90^o\)
\(\Rightarrow\widehat{HAC}=60^o\)
Vì \(\widehat{ABC}=60^o\left(gt\right)\)
Có \(\widehat{HAC}=60^o\left(cmt\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{HAC}=60^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có độ dài cạnh AC=1dm, nếu cạnh AC dài thêm 2cm nữa thì độ dài cạnh AC gấp 2 lần độ dài cạnh BC. Độ dài cạnh AB lớn hơn độ dài cạnh BC 2cm. Khi đó, chu vi hình tam giác ABC là ...(cm
Tứ giác ABCD có ABCD Bˆ = Aˆ +100 , Cˆ = Bˆ +100 ,Dˆ = Cˆ +100 . Tính số đo các góc của tứ giác
Cho tam giác ABC với hai cạnh BC=2cm AC= 8cm. Hãy tìm độ dài canh AB, biết rằng độ dài này là một số chẵn (cm) . tam giác ABC là tam giác gì?
Gọi x là độ dài cạnh còn lại
AC - BC < x < BC + AC
hay 8-2 < x < 8 + 2
6 < x < 10
mà x là số chẵn nên
x = 8cm
hay độ dài của cạnh AB= 8cm
Ta có:
AC = AB = 8cm
nên tam giác ABC cân tại A
Đúng 8
Bình luận (6)
cho tam giác ABC có AB=2cm,BC=7cm. Tính chu vi tam giác ABC biết độ dài cạnh AC là một số nguyên tố
Lời giải:
Theo BĐT tam giác thì:
$AC< AB+AC$ hay $AC< 9$
$BC< AB+AC$ hay $7< 2+AC$ hay $AC>5$ (cm)
Vậy $9> AC> 5$. Mà $AC$ là số nguyên tố nên $AC=7$
Đúng 0
Bình luận (0)
Câu 4:
Vẽ một tam giác vuông ABC có góc A = 90o, AC = 4 cm, góc C = 60o. Trên tia đối của tia AC lấy điểm D sao cho AD = AC
a) C/m △ABD = △ABC
b) △BCD có dạng đặc biệt nào? Vì sao?
c) Tính độ dài các đọan thẳng BC, AB
a: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AD=AC
AB chung
Do đó: ΔABD=ΔABC
b: Ta có: ΔABD=ΔABC
nên BD=BC
=>ΔBCD cân tại B
mà \(\widehat{C}=60^0\)
nên ΔCBD đều
Đúng 0
Bình luận (0)



















