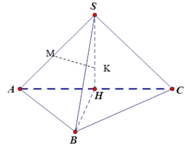
Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A. Biết Smnpq=484cm2. Tính Sabc.

Những câu hỏi liên quan
Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A (hình vẽ). Biết
S
M
N
P
Q
484
c
m
2
. Tính
S
A
B
C
A.
1089
c
m
2
B.
18...
Đọc tiếp
Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A (hình vẽ). Biết S M N P Q = 484 c m 2 . Tính S A B C
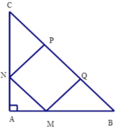
A. 1089 c m 2
B. 1809 c m 2
C. 1089 2 c m 2
D. 2178 c m 2
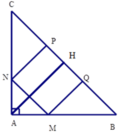
Ta có
Kẻ AH ⊥ BC => H là trung điểm cạnh BC (vì tam giác ABC vuông cân tại A)
Khi đó AH là đường trung tuyến nên AH = B C 2 (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
Xét tam giác vuông CNP có C ^ = 450 (do tam giác ABC vuông cân) nên tam giác CNP vuông cân tại P
Suy ra CP =PN = 22cm
Tương tự ta có ΔQMB vuông cân tại Q => QM = QB = 22cm
Từ đó BC = PC + PQ + QB = 22 + 22 + 22 = 66cm
Mà AH = B C 2 (cmt) => AH = 66 2 = 33cm
Từ đó SABC = 1 2 AH.BC = 1 2 .33.66 = 1089 cm2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
cho hình chóp SABC có tam giác ABC vuông cân tại A, AB=a, tam giác SAB cân tại S. (SAB) vuông góc với (ABC). (SBC) tạo với đáy 1 góc 45°. Tính thể tích SABC
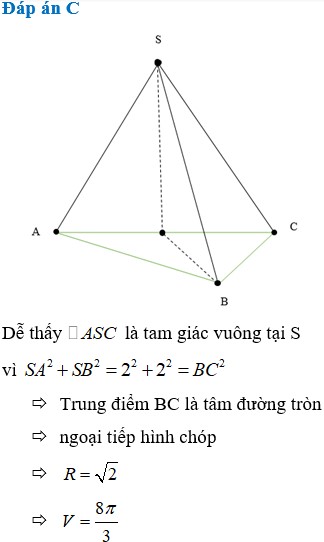
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB2, các cạnh bên đều bằng 2. Tính thể tích của khối cầu ngoại tiếp hình chóp SABC bằng
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=2, các cạnh bên đều bằng 2. Tính thể tích của khối cầu ngoại tiếp hình chóp SABC bằng
![]()
![]()
![]()
![]()
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B,
A
B
2
, các cạnh bên đều bằng 2. Tính thể tích của khối cầu ngoại tiếp hình chóp SABC bằng A.
32
π
3
B.
4
3
π
27
C.
8
2
π...
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, A B = 2 , các cạnh bên đều bằng 2. Tính thể tích của khối cầu ngoại tiếp hình chóp SABC bằng
A. 32 π 3
B. 4 3 π 27
C. 8 2 π 3
D. 8 π 3
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB 2, các cạnh bên đều bằng 2. Tính thể tích V của khối cầu ngoại tiếp hình chóp SABC A.
V
32
π
3
B.
V
4
3
π
27
C.
V
8
2
π...
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB = 2, các cạnh bên đều bằng 2. Tính thể tích V của khối cầu ngoại tiếp hình chóp SABC
A. V = 32 π 3
B. V = 4 3 π 27
C. V = 8 2 π 3
D. V = 8 π 3
Cho tam giác ABC vuông tại A. Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại D. Chứng minh rằng S A B C = BD.DC
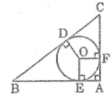
Gọi E và F lần lượt là tiếp điểm của đường tròn với AD và AC
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AE = AF
BE = BD
CD = CF
BD = BC + CD
BE = AB – AE
Suy ra: BD + BE = AB + BC – (AE + CD)
= AB + BC – (AE + CE)
= AB + BC – AC
Suy ra: BD = (AB + BC - AC)/2
Lại có: CD = BC – BD
CF = AC = AF
Suy ra: CD + CF = BC + AC – (BD + AF)
= BC + AC – (BE + AE)
= BC + AC – BA

Vậy S A B C = BD.DC.
Đúng 1
Bình luận (1)
cho tam giác ABC cân tại A nội tiếp (O;10)biết đường cao AH bằng độ dài cạnh BC tính Sabc
Cho hình chóp S.ABC có mp(SAB)
⊥
mp(ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông cân tại S. Tính thể tích hình chóp SABC A.
a
3
3
3
B.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có mp(SAB) ⊥ mp(ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông cân tại S. Tính thể tích hình chóp SABC
A. a 3 3 3
B. a 3 3 6
C. 2 a 3 3 3
D. a 3 3 12
Đáp án là A
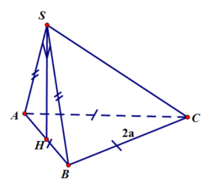
![]()
![]()
![]()
Ta có :
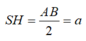
( Do SAB là tam giác vuông cân tại S cạnh huyền AB=2a)
Diện tích tam giác ABC là

Vậy thể tích khối chóp SABC là:
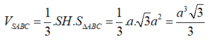
Đúng 0
Bình luận (0)
a,Tính góc giữa SC và ( ABC) b, Tính góc giữa ( SBC ) Và ( ABC) Biết: 1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA asqrt{3}, SB a
Đọc tiếp
a,Tính góc giữa SC và ( ABC)
b, Tính góc giữa ( SBC ) Và ( ABC)
Biết:
1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ
2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA= \(a\sqrt{3}\), SB= a