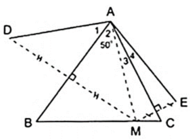
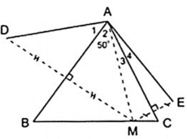
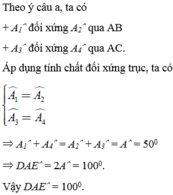2: Cho Δ ABC có Aˆ = 50 0 , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ
điểm E đối xứng với M qua AC.
a) Chứng minh rằng AD = AE.
b) Tính số đo góc DAEˆ =?

Những câu hỏi liên quan
Cho tam giác ABC có góc A=70o, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC
a) Chứng minh rằng AD=AE
b) tính số đo góc DAE
a: Ta có: D đối xứng với M qua AB
nên AD=AM(1)
Ta có: E đối xứng với M qua AC
nên AM=AE(2)
Từ (1) và (2) suy ra AD=AE
Đúng 0
Bình luận (0)
Cho Δ ABC có A ^ = 50 0 , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Chứng minh rằng AD = AE.
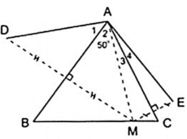
Theo giả thiết ta có:
+ D đối xứng với M qua AB.
+ E đối xứng với M qua AC.
+ A đối xứng với A qua AB, AC.
⇒ AD đối xứng với AM qua AB, AE đối xứng với AM qua AC.
Áp dụng tính chất đối xứng ta có:
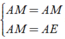
⇒ AD = AE ⇒ (đpcm).
Đúng 0
Bình luận (0)
Cho Δ ABC có A ^ = 50 0 , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Chứng minh rằng AD = AE.
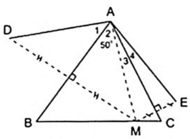
Theo giả thiết ta có:
+ D đối xứng với M qua AB.
+ E đối xứng với M qua AC.
+ A đối xứng với A qua AB, AC.
AD đối xứng với AM qua AB, AE đối xứng với AM qua AC.
⇒ Áp dụng tính chất đối xứng ta có: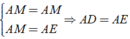
⇒ (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 70^o , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. a. Chứng minh rằng AD = AE b. Tính số đo góc DAE
tự kẻ hình :
AB là đường trung trực của MD (gt)
=> AM = AD (đl) (1)
AC là đường trung trực của EM (gt)
=> AE = AM (đl) (2)
(1)(2) => AE = AD
Đúng 0
Bình luận (0)
a. Vì D đối xứng với M qua trục AB
\(\Rightarrow\) AB là đường trung trực MD.
\(\Rightarrow\) AD = AM (tính chất đường trung trực) (1)
\(\Rightarrow\) Vì E đối xứng với M qua trục AC
\(\Rightarrow\) AC là đường trung trực của ME
\(\Rightarrow\) AM = AE ( tính chất đường trung trực) (2)
\(\Rightarrow\) Từ (1) và (2) suy ra : AD = AE
b ) AD = AM suy ra \(\Delta AMD\) cân tại A có \(AB\perp MD\)
nên AB cũng là đường phân giác của góc MAD
\(\Rightarrow\widehat{A_1}=\widehat{A}_2\)
AM = AE suy ra \(\Delta AME\) cân tại A có \(AC\perp ME\) nên AC cũng là đường phân giác của \(\widehat{MAE}\)
\(\Rightarrow\widehat{A}_3=\widehat{A}_4\)
\(\widehat{DAE}=\widehat{A}_1+\widehat{A}_2+\widehat{A}_3+\widehat{A}_4\)
\(=2\left(\widehat{A}_2+\widehat{A}_3\right)=2\widehat{BAC}=2.70^o=140^o\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Cho Δ ABC có A ^ = 50 0 , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Tính số đo góc D A E ^ = ?
Cho Δ ABC có A ^ = 50 0 , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Tính số đo góc D A E ^ = ?
Cho tam giác ABC có \(\widehat{A}=70^0\), điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC
a) Chứng minh rằng AD = AE
b) Tính số đo góc DAE
a) D đx với m qua AB
=> AB là trung trực của MD
=> AD=AM
E đx với M qua AC
=> AM=AE
=> AD=AE
b) AD=AM => tam giác ADM cân
=>góc DAB =góc MAB
tam giác AME cân
=> góc MAC= góc CAE
do đó: DAB+MAB+MAC+CAE=2(MAB+MAC)=2.70=140 độ
hay góc DAE=140 độ
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A = 70 độ ,điểm M thuộc cạnh BC . Vẽ điểm D đối xứng với M qua AB , vẽ điểm E đối xứng với M qua AC .
a) chứng minh rằng AD =AE
b) tính số đo góc DAE
Bài 5: Cho tam giác ABC nhọn , M là 1 điểm nằm giữa B và C. Gọi D và E lần lượt đối xứng với M qua AB và AC.
a) Chứng minh AD = AE.
b) Tính số đogóc DAE nếu số đo góc BAC là x.
c) Tìm vị trí của M trên BC để DE ngắn nhất.
cs vẽ hình
a: Ta có: M và D đối xứng với nhau qua AB
nên AB là đường trung trực của MD
=>AM=AD(1)
Ta có: M và E đối xứng nhau qua AC
nên AC là đường trung trực của ME
=>AM=AE(2)
Từ (1) và (2) suy ra AD=AE
b: Ta có: ΔADM cân tại A
mà AB là đường cao
nên AB là tia phân giác của góc DAM(1)
Ta có: ΔAEM cân tại A
mà AC là đường cao
nên AC là tia phân giác của góc EAM(2)
Từ (1) và (2) suy ra \(\widehat{DAM}+\widehat{EAM}=2\cdot\widehat{A}=2x\)
hay \(\widehat{DAE}=2\cdot x\)
Đúng 0
Bình luận (0)