Tìm nghiệm của đa thức
a) x2+11x-12
b) 2x2-7x+9
c) x2-12x+20
d) 4x2-13x+3
e) x2-8x-20
Phân tích các đa thức sau thành nhân tử: a) x3 - 2x2 + x b) x2 – 2x – 15 c) 5x2y 3 – 25x3y 4 + 10x3y 3 d) 12x2y – 18xy2 – 30y2 e) 5(x-y) – y.( x – y) g)36 – 12x + x2 h) 4x2 + 12x + 9 i) 11x + 11y – x 2 – xy
Bạn cần viết đề bằng công thức toán để được hỗ trợ tốt hơn.
Bài 2 Tìm nghiệm của các đa thức sau:
a) (x2 – 9)(x + l); b) x2 + 4x – 5;
c) x2+ 9x + 20; d) x2 – x – 20;
e) 2x2 +7x + 6; f) 3x2 + x – 4.
Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
a ) 12 x 2 − 8 x + 1 = 0 ; x 1 = 1 2 b ) 2 x 2 − 7 x − 39 = 0 ; x 1 = − 3 c ) x 2 + x − 2 + 2 = 0 ; x 1 = − 2 d ) x 2 − 2 m x + m − 1 = 0 ; x 1 = 2
Theo định lý Vi-et ta có: phương trình
a
x
2
+
b
x
+
c
= 0 có hai nghiệm
x
1
;
x
2
thì: 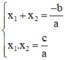
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 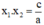
(Các bạn có thể làm cách 2 sử dụng điều kiện 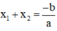 ).
).
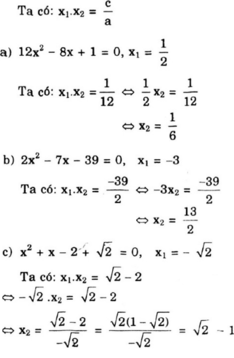
d) x 2 - 2 m x + m - 1 = 0 ( 1 )
Vì x 1 = 2 là một nghiệm của pt (1) nên:
2 2 - 2 m . 2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x 1 . x 2 = m - 1 (hệ thức Vi-ét)
⇔ 2 . x 2 = 0 ( v ì x 1 = 2 và m = 1)
⇔ x 2 = 0
Bài 1: Tìm nghiệm của các đa thức sau:
a) x + 7; b) x – 4; c) –8x + 20; d) x2 – 100;
e) 4x2 – 81; f) x2 – 7; g) x2 – 9x; h) x3 + 3x.
phân tích đa thức thành nhân tử :
a) x2 - 6x +5
b) x2 - x - 12
c) x2 + 8x +15
d) 2x2 - 5x -12
e) x2 - 13x + 36
a: \(x^2-6x+5=\left(x-5\right)\left(x-1\right)\)
b: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
c: \(x^2+8x+15=\left(x+5\right)\left(x+3\right)\)
d: \(2x^2-5x-12=\left(x-4\right)\left(2x+3\right)\)
e: \(x^2-13x+36=\left(x-9\right)\left(x-4\right)\)
3. Tìm nghiệm của các đa thức sau:
a) x + 7; b) \(\dfrac{1}{2}\)x - 4; c) - 8x + 20; d) x2 -100;
e) 4x2 -81; f) x2 - 7; g) x2 - 9x; h) x3 + 3x.
b: 1/2x-4=0
=>1/2x=4
hay x=8
a: x+7=0
=>x=-7
e: 4x2-81=0
=>(2x-9)(2x+9)=0
=>x=9/2 hoặc x=-9/2
g: x2-9x=0
=>x(x-9)=0
=>x=0 hoặc x=9
a)\(x+7=0=>x=-7\)
b)\(\dfrac{1}{2}x-4=0=>\dfrac{1}{2}x=4=>x=8\)
c)\(-8x+20=0=>-8x=-20=>x=\dfrac{5}{2}\)
d)\(x^2-100=0=>x^2=100=>\left[{}\begin{matrix}x=10\\x=-10\end{matrix}\right.\)
e)\(4x^2-81=0=>4x^2=81=>x^2=\dfrac{81}{4}=>\left[{}\begin{matrix}x=\dfrac{9}{2}\\x=-\dfrac{9}{2}\end{matrix}\right.\)
f)\(x^2-7=0=>x^2=7=>x=\sqrt{7}\)
g)\(x^2-9x=0=>x\left(x-9\right)=0=>\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\)
3. Tìm nghiệm của các đa thức sau:
a) x + 7; b) \(\dfrac{1}{2}\)x - 4; c) - 8x + 20; d) x2 -100;
e) 4x2 -81; f) x2 - 7; g) x2 - 9x; h) x3 + 3x.
a: x+7=0
nên x=-7
b: x-4=0
nên x=4
c: -8x+20=0
=>-8x=-20
hay x=5/2
d: x2-100=0
=>(x-10)(x+10)=0
=>x=10 hoặc x=-10
a) x +7 =0
=>x = -7
b) x - 4 =0=>x = 4
c) -8x + 20 = 0 =>-8x =-20 =>\(x=-\dfrac{20}{-8}=\dfrac{5}{2}\)
d)\(x^2-100=0=>x^2=100>\left[{}\begin{matrix}x=10\\x=-10\end{matrix}\right.\)
e)\(4x^2-81=0=>4x^2=81=>x^2=\dfrac{81}{4}=>\left[{}\begin{matrix}x=\dfrac{9}{2}\\x=-\dfrac{9}{2}\end{matrix}\right.\)
f)\(x^2-7=0=>x^2=7=>x=\sqrt{7}\)
g)\(x^2-9x=0=>x\left(x-9\right)=0=>\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\)
H)\(x^3+3x=0=>x\left(x^2 +3\right)=0=>\left[{}\begin{matrix}x=0\\x^2=-3\left(vl\right)\end{matrix}\right.\)
Cho hai đa thức
f ( x ) = - 2 x 2 - 3 x 3 - 5 x + 5 x 3 - x + x 2 + 4 x + 3 + 4 x 2 , g ( x ) = 2 x 2 - x 3 + 3 x + 3 x 3 + x 2 - x - 9 x + 2
c. Tìm nghiệm của h(x)
c. Ta có h(x) = 0 ⇒ 5x + 1 = 0 ⇒ x = -1/5
Vậy nghiệm của đa thức h(x) là x = -1/5 (1 điểm)
Tính.
a, (x3-2x2-10x-7):(x2-7-3x)
b, (x3+4x2+8x+5):(x+1)
c, (x3-x2-13x-14):(x2-3x-7)
d, (x3+5x2+5x):(x+5)
a: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)
b:\(=\dfrac{x^3+x^2+3x^2+3x+5x+5}{x+1}=x^2+3x+5\)
c:\(=\dfrac{x^3-3x^2-7x+2x^2-6x-14}{x^2-3x-7}=x+2\)
d: \(=\dfrac{x^2\left(x+5\right)+5x+25-25}{x+5}=x^2+5-\dfrac{25}{x+5}\)