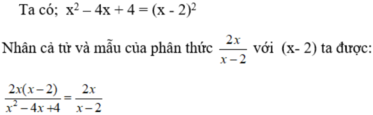Nêu hai cách điền vào chỗ trống của biểu thức x4 + x2 + ... để được bình phương của một tổng hoặc một hiệu.

Những câu hỏi liên quan
Điền vào chỗ chống để các biểu thức sau trở thành bình phương của một tổng hoặc 1 hiệu
a) x2 +20x+.......
b)16 x2+24xy+.......
c)y2-.......+49
d)......-42xy+49y2
`a)x^2+20x+100=(x+10)^2`
`b)16x^2+24xy+9y^2=(4x+3y)^2`
`c)y^2-14y+49=(y-7)^2`
`d)9x^2-42xy+49y^2=(3x-7y)^2`
Đúng 3
Bình luận (0)
a, \(x^2+2x.10+100=\left(x+10\right)^2\)
\(b,16x^2+2.4x.3y+9y^2=\left(4x+3y\right)^2\)
\(c,y^2-14y+49=\left(y-7\right)^2\)
\(d,9x^2-2.3x.7x+49y^2=\left(3x-7y\right)^2\)
Đúng 3
Bình luận (0)
điền biểu thức thích hợp vào dấu? để biểu thức trở thành bình phương của một tổng hay một hiệu :
a)(?-?)=a^2-6ab+?
b)(?+?)^2=?+m+1/4
Điền hạng tử thích hợp vào chỗ có dấu sao để mỗi đa thức sau trở thành hàng đẳng thức bình phương 1 tổng hoặc hiệu của 1 tích
a, x2+ 20x + *
b,y2- * +49
Giúp mk vs mk đg cần gấp
a) x2+20x+* = \(x^2+2.x.10+10^2=\left(x+10\right)^2\)
b) \(y^2-2.y.7+7^2=y^2-14y+49=\left(y-7\right)^2\)
Đúng 0
Bình luận (0)
Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:a)
x
2
+ 2x + 1; b) -8x + 16 +
x
2
;c)
x
2
4
+
x
+
1
;
d) 4
x
2
+ 4
y
2
– 8xy.
Đọc tiếp
Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:
a) x 2 + 2x + 1; b) -8x + 16 + x 2 ;
c) x 2 4 + x + 1 ; d) 4 x 2 + 4 y 2 – 8xy.
a) ( x + 1 ) 2 . b) ( x – 4 ) 2 .
c) x 2 4 + x + 1 ; d) ( 2 x – 2 y ) 2 .
Đúng 0
Bình luận (0)
Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tống hoặc một hiệu, rồi điền chữ dòng với biểu thức đó vào bảng cho thích hợp. Sau khi thêm dấu, em sẽ tìm ra một trong những đức tính quý báu của con người.x3 – 3x2 + 3x – 116 + 8x + x23x2 + 3x + 1 + x31 – 2y + y2NUHÂ(x – 1)3(x + 1)3(y – 1)2(x – 1)3(1 + x)3(1 – y)2(x + 4)2
Đọc tiếp
Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tống hoặc một hiệu, rồi điền chữ dòng với biểu thức đó vào bảng cho thích hợp. Sau khi thêm dấu, em sẽ tìm ra một trong những đức tính quý báu của con người.
x3 – 3x2 + 3x – 1 16 + 8x + x2 3x2 + 3x + 1 + x3 1 – 2y + y2 | N U H Â |
| (x – 1)3 | (x + 1)3 | (y – 1)2 | (x – 1)3 | (1 + x)3 | (1 – y)2 | (x + 4)2 |
\(x^3-3x^2+3x-1=\left(x-1\right)^3\)
\(x^2+8x+16=\left(x+4\right)^2\)
\(x^3+3x^2+3x+1=\left(x+1\right)^3\)
\(1-2x+x^2=\left(x-1\right)^2\)
Đúng 1
Bình luận (0)
Hãy điền vào chỗ trống một đa thức thích hợp để được đẳng thức:
2
x
.
.
.
.
x
2
-
4
x
+
4
2
x
x...
Đọc tiếp
Hãy điền vào chỗ trống một đa thức thích hợp để được đẳng thức: 2 x . . . . x 2 - 4 x + 4 = 2 x x - 2
Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:a) 4
x
2
+ 4x + 1; b) 9
x
2
– 12x + 4;c)
ab
2
+
1
4
a
2
b
4
+
1
;
d)
16
u
2
v...
Đọc tiếp
Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:
a) 4 x 2 + 4x + 1; b) 9 x 2 – 12x + 4;
c) ab 2 + 1 4 a 2 b 4 + 1 ; d) 16 u 2 v 4 − 8 uv + 2 1 .
a) ( 2 x + 1 ) 2 . b) ( 3 x – 2 ) 2 .
c) 1 2 ab 2 + 1 2 . d) ( 4 uv 2 – 1 ) 2 .
Đúng 0
Bình luận (0)
. Điền các đơn thức thích hợp vào chỗ trống để đa thức sau là bình phương của một đa thức hoặc đơn thức với hệ số nguyên, trong mỗi trường hợp hãy viết từng đẳng thức minh họa cụ thể: 16x4 + 16x2y2 + ...
ta viết : 16x4 + 16x2y2 + 4y4
= (4x2)2 + 2 . 4x2 . 2y2 + (2y2)2
= ( 4x2 + 2y2 )2
Đúng 0
Bình luận (0)
Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu
a . x2 -6xy +9y2
\(x^2-6xy+9y^2\)
\(=x^2-2\cdot3y\cdot x+\left(3y\right)^2\)
\(=\left(x-3y\right)^2\)
Đúng 2
Bình luận (0)
viết các đa thức sau dưới dạng bình phương của một tổng hoặc hiệu
4x2 + 4x + 1
Đúng 0
Bình luận (0)