Cho hình thoi ABCD. Biết góc A = 60 độ, M và N là trung điểm của AD và CD. Tính số đo góc BMN

Những câu hỏi liên quan
Cho hình thoi ABCD(gócA<90độ) trên AD lấy M , trên CD lấy N sao cho AM=CN a) chứng minh tam giác BMN cân. b) chứng minh BD vuông góc với MN. c) biết góc A =60 độ ,M và N lần lượt là trung điểm của AD và CD,tính số đo góc BMN
a: Xét ΔBAM và ΔBCN có
BA=BC
góc BAM=góc BCN
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
=>ΔBMN cân tại B
b: DM+MA=DA
DN+NC=DC
mà DA=DC và MA=NC
nên DM=DN
BM=BN
DM=DN
Do đó: BD là trung trực của MN
=>BD vuông góc MN
c: Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
ΔABD đều có BM là trung tuyến
nên BM là phân giác của góc ABD(1)
Xét ΔCBD có CB=CD và góc C=60 độ
nên ΔCBD đều
ΔCBD đều có BN là trung tuyến
nên BN là phân giác của góc DBC(2)
Từ (1), (2) suy ra góc MBN=1/2(góc ABD+góc CBD)
=1/2*góc ABC
=60 độ
Xét ΔBMN có BM=BN và góc MBN=60 độ
nên ΔBMN đều
=>góc BMN=60 độ
Đúng 0
Bình luận (0)
cho hình thoi ABCD có độ cạnh dài 4 cm góc A =60 độ gọi M,N lần lượt là trung điểm của AD và CD
a)CMtam giác BMN là tam giác đều
b)tính chu vi tam giác BMN
cho hình thoi ABCD có góc a bằng 60 độ .trên AD lấy điểm M, trên CD lấy điểm N sao cho AM=DN. Tam giác BMN là tam giác gì
1.Hình chữ nhật ABCD,BH vuông góc với AC,M và K là trung điểm AH,CD. Tính góc BMK
2.Hình thoi ABCD,một góc 60 độ. trên AD và CD lấy M,N. Tổng AM và CN là AD.P đối xứng N qua BC. chứng minh MP song song CD
1.Hình chữ nhật ABCD,BH vuông góc với AC,M và K là trung điểm AH,CD. Tính góc BMK
2.Hình thoi ABCD,một góc 60 độ. trên AD và CD lấy M,N. Tổng AM và CN là AD.P đối xứng N qua BC. chứng minh MP song song CD
Cho hình chóp S.ABCD có ABCD là hình thoi tâm O cạnh a, góc ABC = 60 độ. Hình chiếu vuông góc của S lên (ABCD) là trung điểm của OB, SC tạo với (ABCD) góc 60 độ. Gọi M là trung điểm CD. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AM và SB
cho hình thoi abcd có góc b là góc tù . kẻ bm và bn thứ tự vuông góc với ad và cd tại m,n . biết mn/bd=1/2 .tính số đo các góc của hình thoi
cho hình thoi ABCD có góc A=60 độ, gọi P là trung điểm của AB, N là giao điểm của đường thẳng AD và CD. CMR:
a) diện tích hình thoi = 4diện tích tam giác PBC
b) gọi N là giao điểm của BN và DP. CM: PA.PB=PD.PM
Hình thoi ABCD có góc A = 60°. Trên cạnh AD lấy điểm M, trên cạnh CD lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì? Vì sao?
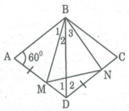
Nối BD, ta có AB = AD (gt)
Suy ra ∆ ABD cân tại A
Mà ∠ A = 60 0 ⇒ ∆ ABD đều
⇒ ∠ (ABD) = ∠ D 1 = 60 0 và BD = AB
Suy ra: BD = BC = CD
⇒ ∆ CBD đều ⇒ ∠ D 2 = 60 0
Xét ∆ BAM và ∆ BDN,ta có:
AB = BD ( chứng minh trên)
∠ A = ∠ D 2 = 60 0
AM = DN (giả thiết)
Do đó ∆ BAM = ∆ BDN ( c.g.c) ⇒ ∠ B 1 = ∠ B 3 và BM = BN
Suy ra ΔBMN cân tại B.
Mà ∠ B 2 + ∠ B 1 = ∠ (ABD) = 60 0
Suy ra: ∠ B 2 + ∠ B 3 = ∠ B 2 + ∠ B 1 = 60° hay ∠ (MBN) = 60 0
Vậy ∆ BMN đều
Đúng 1
Bình luận (0)















