(2x-1)(y-4)=-13
Tìm giá trị nguyên x,y
Những câu hỏi liên quan
TÌm các số nguyên x,y thỏa mãn : 2x^2+1/x^2 +y^2/4 =4 sao cho tích x,y đạt giá trị lớn nhất
\(\text{Ta có : }2x^2+\frac{1}{x^2}+\frac{y^2}{4}=4\)
\(\Leftrightarrow\left(x^2+2+\frac{1}{x^2}\right)+\left(x^2-xy+\frac{y^2}{4}\right)=2-xy\)
\(\Leftrightarrow\left(x+\frac{1}{x}\right)^2+\left(x-\frac{y}{2}\right)^2=2-xy\)
\(\text{ Lại có : }\left(x+\frac{1}{x}\right)^2+\left(x-\frac{y}{2}\right)^2\ge0\)
\(\Rightarrow2-xy\ge0\)
\(\Rightarrow xy\le2\)
Mà xy có giá trị lớn nhất
\(\Rightarrow xy\in\left\{\left(1;2\right)\left(2;1\right)\left(-1;-2\right)\left(-2;-1\right)\right\}\)
Tìm các số nguyên x,y thỏa mãn:6xy+4x-9y-7=0
Tìm giá trị nhỏ nhất của A=x^3+y^3+xy với x,y dương thỏa mãn x+y=1
Tìm các số nguyên x,y thỏa mãn 2x^2+1/x^2+y^2/4=4 sao cho xy đạt giá trị lớn nhất
HELP !
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
Đúng 0
Bình luận (0)
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Xác định a sao cho 10x^2-7x+a chia hết cho 2x-3 .giá trị a là?
Tìm x để giá trị nguyên A=(x+2)/(x^2+4) nguyên ?
giá trị nhỏ nhất P=(x^4+1)(y^4+1) biết x+y= căn 10
trình bày dùm mình với nha
Xem chi tiết
Tìm x để giá trị nguyên A=(x+2)/(x^2+4) nguyên ?
giá trị nhỏ nhất P=(x^4+1)(y^4+1) biết x+y= căn 10
trình bày dùm mình với nha
Câu 1:
\(\Leftrightarrow10x^2-15x+8x-12+a+12⋮2x-3\)
=>a+12=0
hay a=-12
Câu 2;
Để A là số nguyên thì \(\left(x+2\right)⋮x^2+4\)
\(\Leftrightarrow x^2-4⋮x^2+4\)
\(\Leftrightarrow x^2+4-8⋮x^2+4\)
\(\Leftrightarrow x^2+4\in\left\{4;8\right\}\)
hay \(x\in\left\{0;2;-2\right\}\)
Đúng 0
Bình luận (0)
1/ Giá trị của x^3+ 9x^2y+ 27xy^2+27y^3 Biết (1/3)x+y+1=0
2/Giá trị của x+y=4, x.y=5 và x<0
3/Giá trị của 8x^3- 12x^2y-6xy^2-y^3
4/Giá trị x nguyên tố thỏa mản: x^2-x-20=0
5/Giá trị của x thỏa mãn (x-3)(x^4+2x^2+1)=0
6/Giá trị nhỏ nhất của: A=[x+2]-51/2
vì x+y=4 nền (x+y)^2=4^2 =x^2+ 2xy+y^2=16 ma xy=5 nên 2xy=10 ta có x^2+y^2+10=16 ; x^2+y^2= 16-10 x^2+y^2=6 kết quả mik là z đó nhưng k biết có đúng k bn ak
Đúng 0
Bình luận (0)
1/ Giá trị của x^3+ 9x^2y+ 27xy^2+27y^3 Biết (1/3)x+y+1=0
2/Giá trị của x+y=4, x.y=5 và x<0
3/Giá trị của 8x^3- 12x^2y-6xy^2-y^3
4/Giá trị x nguyên tố thỏa mản: x^2-x-20=0
5/Giá trị của x thỏa mãn (x-3)(x^4+2x^2+1)=0
6/Giá trị nhỏ nhất của: A=[x+2]-51/2
Tìm các cặp số nguyên (x;y) thoả mãn 2x^2+1/x^2+y^2/4=4 sao cho tích x.y đạt giá trị lớn nhất
Cho các số thực dương x, y thỏa mãn
x
2
+
x
x
+
1
y
+
2
x
+
1
y
+
1
. Gọi M, m lần lượt là giá trị lớn nhất, giá t...
Đọc tiếp
Cho các số thực dương x, y thỏa mãn x 2 + x x + 1 = y + 2 x + 1 y + 1 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = - x 2 + x + 4 + 4 - x 2 - x + 1 y + 1 + a . Có bao nhiêu giá trị nguyên của tham số a ∈ - 10 ; 10 để M ≤ 2 m
A. 4
B. 5
C. 6
D. 7
Chọn đáp án B
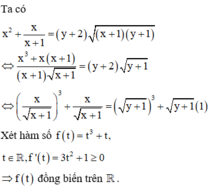
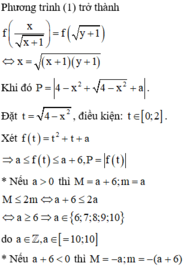
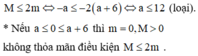
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
Đúng 0
Bình luận (0)
1- Tính :
A= 5. | x- 5 | - 3x + 1
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------
Giup mình với ah.
1- Tính :
A= 5. | x- 5 | - 3x + 1
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------
Đúng 0
Bình luận (0)
bài 1:
a) Tìm các cẶP số nguyên x; y thỏa mãn hệ thức: ( 2x - 1 ) (y + 4 ) = 11
b) Tìm các giá trị x;y nguyên thỏa mãn: xy = 3y - 5x = 9
11=1x11=11x1=-1x-11=-11x-1
TH1:
2x-1=1 y+4=11
2x=2 y=7
x=1
TH2:
2x-1=11 y+4=1
2x=12 y=-5
x=6
TH3:
2x-1=-1 y+4=-11
2x=-2 y=-15
x=-1
TH4:
2x-1=-11 y+4=-1
2x=-10 y=-5
x=-5
Đúng 0
Bình luận (0)
a)(2x-1)(y+4)=11
Ta có:11=1.11=11.1=(-1).(-11)=(-11).(-1)
Do đó ta có bảng sau:
| y+4 | -11 | -1 | 1 | 11 |
| 2x-1 | -1 | -11 | 11 | 1 |
| 2x | 0 | -10 | 12 | 2 |
| x | 0 | -5 | 6 | 1 |
| y | -15 | -5 | -3 | 7 |
Vậy các cặp (x;y) TM là:(0;-15)(-5;-5)(6;-3)(1;7)
Đúng 0
Bình luận (0)