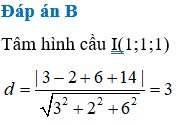cho 3 số x2+2y+1=y2+2z+1=z2+2x+1+0.tính: A=x2017+y2018+z2019

Những câu hỏi liên quan
Trong không gian Oxyz cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
2
y
-
2
z
-
22
0
và mặt phẳng (P): 3x-2y+5z+10. Tính khoảng cách h từ tâm của (S) tới (P) A. h4 B. h3 C. h2 D. h1
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z - 22 = 0 và mặt phẳng (P): 3x-2y+5z+1=0. Tính khoảng cách h từ tâm của (S) tới (P)
A. h=4
B. h=3
C. h=2
D. h=1
Vị trí tương đối của hai mặt cầu:
x
2
+
y
2
+
z
2
+ 2x - 2y - 2z - 7 0 và
x
2
+
y
2
+
z
2
+ 2x + 2y + 4z + 5 0 là: A. ở ngoài nhau B. tiếp xúc C. cắt nhau D....
Đọc tiếp
Vị trí tương đối của hai mặt cầu: x 2 + y 2 + z 2 + 2x - 2y - 2z - 7 = 0 và x 2 + y 2 + z 2 + 2x + 2y + 4z + 5 = 0 là:
A. ở ngoài nhau
B. tiếp xúc
C. cắt nhau
D. chứa nhau
Đáp án C
Mặt cầu: x 2 + y 2 + z 2 + 2x - 2y – 2z – 7 = 0 có tâm I(-1; 1;1) và
Mặt cầu: x 2 + y 2 + z 2 + 2x + 2y + 4z + 5= 0 có tâm I’( -1; -1; -2) và R’ = 1
![]()
Do đó, hai mặt cầu này cắt nhau.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho 3 điểm
A
6
;
0
;
0
;
B
0
;
6
;
0
;
C
0
;
0
;
6
.
Hai mặt cầu có phương trình...
Đọc tiếp
Trong không gian Oxyz, cho 3 điểm A 6 ; 0 ; 0 ; B 0 ; 6 ; 0 ; C 0 ; 0 ; 6 . Hai mặt cầu có phương trình S 1 : x 2 + y 2 + z 2 − 2 x − 2 y + 1 = 0 và S 2 : x 2 + y 2 + z 2 − 8 x + 2 y + 2 z + 1 = 0 cắt nhau theo đường tròn (C). Hỏi có bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa (C) và tiếp xúc với ba đường thẳng AB, BC, CA?
A. 4
B. Vô số
C. 1
D. 3
Cho mặt phẳng (P): 2x+2y-2z+150 và mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
y
-
2
z
-
1
0
. Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu(S) là A.
3
3
2
B...
Đọc tiếp
Cho mặt phẳng (P): 2x+2y-2z+15=0 và mặt cầu (S): x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 . Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu(S) là
A. 3 3 2
B. 3
C. 3 2
D. 3 3
Viết phương trình mặt phẳng song song với (P): 6x -2y + 3z + 7 0 và tiếp xúc với mặt cầu
x
2
+
y
2
+
z
2
+2x+2y+2z - 1 0 A. 6x - 2y + 3z - 8 0 B. 6x - 2y + 3z - 3 0 C. 6x - 2y + 3z -7 0 D. 6x - 2y + 3z - 5 0
Đọc tiếp
Viết phương trình mặt phẳng song song với (P): 6x -2y + 3z + 7 = 0 và tiếp xúc với mặt cầu x 2 + y 2 + z 2 +2x+2y+2z - 1 = 0
A. 6x - 2y + 3z - 8 = 0
B. 6x - 2y + 3z - 3 = 0
C. 6x - 2y + 3z -7 = 0
D. 6x - 2y + 3z - 5 = 0
Chọn C
Gọi (Q) là mặt phẳng cần tìm. Vì (Q) song song với (P) nên phương trình (Q) có dạng
6x - 2y + 3z + a = 0
Tâm mặt cầu I(-1;-1;-1) bán kính R = 2
Vì (Q) tiếp xúc với mặt cầu nên d(I,(Q))=R hay
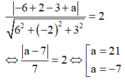
Đúng 0
Bình luận (0)
Viết phương trình mặt phẳng song song với
P
:
6
x
-
2
y
+
3
z
+
7
0
và tiếp xúc với mặt cầu
x
2
+
y
2
+
z
2
+
2
x
+
2
y
+
2
z
-
1...
Đọc tiếp
Viết phương trình mặt phẳng song song với P : 6 x - 2 y + 3 z + 7 = 0 và tiếp xúc với mặt cầu x 2 + y 2 + z 2 + 2 x + 2 y + 2 z - 1 = 0
A. 6 x - 2 y + 3 z - 8 = 0
B. 6 x - 2 y + 3 z - 3 = 0
C. 6 x - 2 y + 3 z - 7 = 0
D. 6 x - 2 y + 3 z - 5 = 0
Đáp án C
Gọi (Q) là mặt phẳng cần tìm. Vì (Q) song song với (P) nên phương trình (Q) có dạng
![]()
Tâm mặt cầu I(-1;-1;-1) bán kính R = 2
Vì (Q) tiếp xúc với mặt cầu nên d(I,(Q)) = R hay
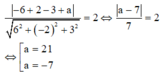
Đúng 0
Bình luận (0)
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng
(
Q
)
:
x
+
2
y
–
2
z
+
1
0
và tiếp xúc với mặt cầu
(
S
)
:
x
2
+
y
2...
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y – 2 z + 1 = 0 và tiếp xúc với mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x – 4 y – 2 z – 3 = 0
A. x + 2 y – 2 z + 6 = 0 ; x + 2 y – 2 z – 12 = 0
B. x + 2 y – 2 z + 8 = 0 ; x + 2 y – 2 z – 10 = 0
C. x + 2 y – 2 z + 10 = 0 ; x + 2 y – 2 z – 8 = 0 .
D. x + 2 y – 2 z + 12 = 0 ; x + 2 y – 2 z – 6 = 0
Chọn C.
Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.

Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng
(
Q
)
:
x
+
2
y
-
2
z
+
1
0
và tiếp xúc với mặt cầu
(
S
)
:
x
2
+
y
2
+...
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y - 2 z + 1 = 0 và tiếp xúc với mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x – 4 y – 2 z – 3 = 0
A. x + 2 y – 2 z + 12 = 0 v à x + 2 y – 2 z - 6 = 0
B. x + 2 y – 2 z – 12 = 0 v à x + 2 y – 2 z + 6 = 0
C. x + 2 y – 2 z + 10 = 0 v à x + 2 y – 2 z - 8 = 0
D. x + 2 y – 2 z – 10 = 0 v à x + 2 y – 2 z + 8 = 0
Chọn D.
Mặt cầu (S) có tâm I(-1;2;1) và bán kính
![]()
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng:
x + 2y – 2z + D = 0 với D ≠ 1.
Vì (P) tiếp xúc với mặt cầu (S) nên d(I;(P)) = R = 3
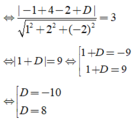
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z – 10 = 0 và x + 2y – 2z + 8 = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
y
-
2
z
-
1
0
và mặt phẳng
P
:
2
x
+
2
y
-
2
z
+
15...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 và mặt phẳng P : 2 x + 2 y - 2 z + 15 = 0 . Khoảng cách ngắn nhất giữa điểm (M) trên (S) và điểm N trên (P) bằng
A. 3 3 2
B. 3 2 3
C. 3 2
D. 2 3
Mặt cầu (S) có tâm I(0;1;1) và bán kính R = 3
Ta có 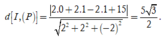
Vậy khoảng cách ngắn nhất: ![]()
Chọn A.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-2z+150 và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
y
-
2
z
-
1
0
Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-2z+15=0 và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là
A. 3 3 2
B. 3
C. 3 2
D. 3 3