cho hình vuông abcd trên cạnh ab lấy điểm m,hai đường thăng dm và cb cắt nhau tại k; cm cắt ak tại n . chứng minh bn vuông góc dk

Những câu hỏi liên quan
cho hình vuông ABCD, trên cạnh AB lấy điểm M, 2 đường thẳng MD và CB cát nhau tại K, CM cắt AK tại N. CMR: BN vuông góc DK
Cho hình vuông ABCD,trên AB lấy đ M, DM cắt CB tại K,CM cắt AK tại N. CMR:BN vuông góc DK
Xem chi tiết
Cho hình vuông ABCD. Trên canh AB lấy điểm M(M#A), trên tia đối của tia CB lấy điểm N Sao cho AM=CN. Gọi E là trung điểm MN, tia DE cắt BC tại F, DM cắt CB tại K. Qua M ve đường thẳng song song với AD cắt DF tại H. CMR:
a) Tứ giác MFNH là hình thoi
b) ND2=NB.NF
c)1/DM2+1/DK2 có giá trị không đổi khi M thay đổi trên AB
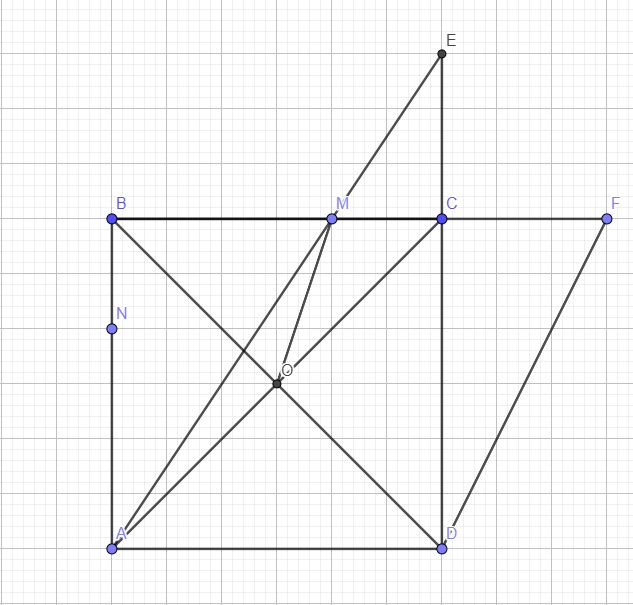
Cho hình vuông ABCD . Trên cạnh BC lấy điểm M (khác B và C) . Trên cạnh AB lấy điểm N sao cho: BN CM . Đường thẳng AM cắt CD tại E .Trên tia đối của tia CB lấy điểm F sao cho CF CE. Gọi O là giao điểm của AC và BD .Chứng minh hai tam giác BOM và BFD đồng dạng.
Đọc tiếp
Cho hình vuông ABCD . Trên cạnh BC lấy điểm M (khác B và C) . Trên cạnh AB lấy điểm N sao cho: BN = CM . Đường thẳng AM cắt CD tại E .Trên tia đối của tia CB lấy điểm F sao cho CF = CE. Gọi O là giao điểm của AC và BD .
Chứng minh hai tam giác BOM và BFD đồng dạng.
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)
Đúng 2
Bình luận (2)
Câu 10. Cho ABCD là hình chữ nhật, AB = 10cm, BC = 6cm. Trên cạnh AB lấy điểm M sao cho AM = 4cm. DM kéo dài cắt CB kéo dài tại K. Tính diện tích KMB ?
Bài 1:
Cho hình vuông ABCD, trên cạnh AB lấy điểm M. Kẻ DM cắt BC tại K, CM cắt AK tại N. Chứng minh BN vuông góc DK
Ta thấy góc BNK = 90o
=> BN vuông góc vs DK ( đpcm )
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Trên cạnh AB lấy điểm M, cạnh AD lấy điểm N sao cho AM = AN. Kẻ AH vuông góc vs DM và AH cắt BC tại P. chứng mình 5 điểm C,D,N,H,P cùng thuộc một đường tròn
làm tương tự
Cho hình vuông ABCD. Gọi O là giao điểm của hai đường chéo AC và BD, M là trung điểm của OB, N là trung điểm của CD.
a, Chứng minh: +góc AMN vuông.
+A, M, N, D cùng thuộc một đường tròn, xác định tâm của nó.
+ AN>MD
b, Trên AB, AD thứ tự lấy I, K sao AI=Ak. Kẻ AP vuông góc DI, cắt BC tại Q. Chứng minh 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn
Bài làm
Từ M hạ ME vuông góc AD,MF vuông góc DC (ME//AB, MF//BC) , nối MA và MN ta có DM = 3/4.DB => AE = CF = 1/4 AD ( AD = DC= AB = BC cạnh hình vuông)
ME = MF = 3/4.AB, NC = 1/2.DC và CF = 1/4 DC => NF = 1/4 DC
=> tam giác vuông AEM = tam giác vuông NFM ( hai cặp cạnh góc vuông bằng nhau đôi một)
=>góc AME = góc NMF mà góc NMF + góc EMN = 90 độ => góc AME + góc EMN = 90 độ
=> góc AMN = 90 độ (điều phải cm)
Gọi I là trung điểm AN, do tam giác ADN vuông tại D =>ID= IA = IN (trung tuyến thuộc cạnh huyền bằng 1/2 cạnh huyền) , tương tự có tam giác AMN vuông tại M => IM = IA = IN
=> 4 điểm A, D, N, M cách đều I => A, M, N, D cùng thuộc một đường tròn tâm là trung điểm I của đoạn AN
tam giác vuông cân DEM có DM^2 = 2.ME^2
tam giác vuông cân AMN có AN^2 = 2.MA^2 mà MA > ME
=> AN^2 > DM^2 => AN > DM (điều phải cm)
b, Trên AB, AD thứ tự lấy I, K sao AI=Ak. Kẻ AP vuông góc DI, cắt BC tại Q. Chứng minh 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn
góc DPQ = 90 độ (theo cách dựng AP vuông góc DI)
và góc DCQ = 90 độ (gt ABCD là hình vuông) nên D, P, C, Q thuộc đường tròn đường kính DQ.
ta sẽ c/m K thuộc đường tròn đường kính DQ.nghĩa là góc DKQ = 90 độ
xét tứ giác IPQB có góc P và B vuông => góc PQB + góc PIB = 180 độ
mà góc góc PIB + góc PIA = 180 độ =>góc PIA =góc PQB => góc DIA = góc AQB
xét 2 tam giác vuông DAI và ABQ có AD = AB và góc DIA = góc AQB
=> tam giác DAI = tam giác ABQ ( cạnh góc vuông, góc nhọn) => AK = BQ => KQ//AB
=> góc DKQ = 90 độ => K thuộc đường tròn đường kính DQ.
=> 5 điểm C, D, K, P, Q cùng nằm trên một đường tròn ( điều phải c/m)
Đúng 0
Bình luận (0)
AH vuông góc DM
=>góc MAH=góc MDA
Xét ΔABP vuông tại B và ΔDAM vuông tại A có
AB=AD
góc MAH=góc MDA
=>ΔABP=ΔDAM
=>BP=AM=AN
mà BC=AD
nên PC=ND
=>PCND là hình chữ nhật
=>P,C,D,N cùng nằm trên đường tròn đường kính DP
mà H nằm trên đường tròn đường kính DP(góc DHP=90 độ)
nên C,D,N,H,P cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD (AB BC). Lấy điểm M tuỳ ý trên cạnh AB (M ≠ A , M ≠ B). Đường thẳng DM cắt AC tại K và cắt đường thẳng BC tại N. a) Chứng minh: NMB đồng dạng với NDC , AKD đồng dạng với CKN b) Chứng minh: KD2 KM.KN c) Biết NB 6 ; NC 15 ; MB 4 : Tìm tỉ số đồng dạng của : NMB và NDC , Tính diện tích của hình chữ nhật ABCD.
Đọc tiếp
Cho hình bình hành ABCD (AB > BC). Lấy điểm M tuỳ ý trên cạnh AB (M ≠ A , M ≠ B). Đường thẳng DM cắt AC tại K và cắt đường thẳng BC tại N. a) Chứng minh: NMB đồng dạng với NDC , AKD đồng dạng với CKN b) Chứng minh: KD2 = KM.KN c) Biết NB = 6 ; NC = 15 ; MB = 4 : Tìm tỉ số đồng dạng của : NMB và NDC , Tính diện tích của hình chữ nhật ABCD.
a. vì ABCD là hình bình hành => MB//CD
theo hệ quả của định lý Ta-lét, ta có: tam giác NMB ~ tam giác NDC
vì AD//CN (ABCD là hbh)
=> \(\dfrac{AK}{KC}\)= \(\dfrac{KD}{KN}\)
góc AKD = góc NKC (đối đỉnh)
=> tam giác AKD ~ tam giác CKN (c.g.c)
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD (AB>). Lấy điểm M tùy ý trên cạnh AB. Đường thẳng DM cắt AC tại K và cắt đường thẳng BC ở N .
1) Chứng minh tgiac ADK ∽ tgiac CNK
2) Chứng minh KM.KC=KD.KA
1: Xét ΔADK và ΔCNK có
góc AKD=góc CKN
góc DAK=góc NCK
=>ΔADK đồng dạng với ΔCNK
2: Xét ΔKAM và ΔKCD có
góc KAM=góc KCD
góc AKM=góc CKD
=>ΔKAM đồng dạng với ΔKCD
=>KA/KC=KM/KD
=>KA*KD=KM*KC
Đúng 0
Bình luận (0)