giải phương trình
a) 7x2-2x+3=0
b)2x2-7x+3=0
Giải phương trình
a) 2x4-7x2+4=0
b) (x2-9)(x2+7x+6)=0
c) 5x4+2x2–16=10–x2
d)√x-5 =x-7
a) Đặt \(x^2=a\left(a\ge0\right)\)
Ta có: \(2x^4-7x^2+4=0\)
Suy ra: \(2a^2-7a+4=0\)
\(\Delta=49-4\cdot2\cdot4=49-32=17\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{7-\sqrt{17}}{4}\left(nhận\right)\\a_2=\dfrac{-7+\sqrt{17}}{4}\left(loại\right)\end{matrix}\right.\)
Suy ra: \(x^2=\dfrac{7-\sqrt{17}}{4}\)
\(\Leftrightarrow x=\pm\dfrac{\sqrt{7-\sqrt{17}}}{2}\)
Vậy: \(S=\left\{\dfrac{\sqrt{7-\sqrt{17}}}{2};-\dfrac{\sqrt{7-\sqrt{17}}}{2}\right\}\)
Bài 1 : giải phương trình
a) 7x-63=0
b)3x+15=0
c) 2x-5
d) -6x+16=0
a: =>7x=63
hay x=9
b: =>3x=-15
hay x=-5
d: =>-6x=-16
hay x=8/3
a) \(7x=63\Leftrightarrow x=9\)
b) \(3x=-15\Leftrightarrow x=-5\)
c) \(2x-5=0\Leftrightarrow2x=5\Leftrightarrow x=\dfrac{5}{2}\)
d) \(-6x=-16\Leftrightarrow x=\dfrac{8}{3}\)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
7 x 2 − 2 x + 3 = 0 b ) 5 x 2 + 2 10 x + 2 = 0 c ) 1 2 x 2 + 7 x + 2 3 = 0 d ) 1 , 7 x 2 − 1 , 2 x − 2 , 1 = 0
a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai 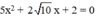
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai 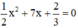
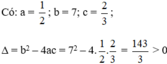
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 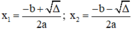
+ Nếu Δ = 0, phương trình có nghiệm kép 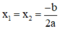 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.
1) Giải hệ phương trình : \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\)
2) Giải phương trình
a) 3x2 - 2x - 1 = 0
b) x4 - 20x2 + 4 = 0
1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
Vậy hpt có nghiệm (x;y) = (3;4)
2)
a) 3x2 - 2x - 1 = 0
\(\Leftrightarrow3x^2-3x+x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)
Vậy pt có nghiệm x = 1 hoặc x = 3
b) Đặt x2 = t (t \(\ge\) 0)
Pt trở thành: t2 - 20t + 4 = 0
\(\Delta\) = (-20)2 - 4.1.4 = 400 - 16 = 384
=> pt có 2 nghiệm phân biệt t1 = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)
t2 = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)
=> x1 = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)
x2 = \(2-\sqrt{6}\)
Giải các pt sau
a) 3x2 + 4x = 0
b) -2x2 - 8 = 0
c) 2x2 -7x2 + 5 = 0
d) x^2 - 8x - 48 = 0
cho mik hỏi rằng là 3x2 + 4x = 0 hay 3x2 + 4x = 0
ông ơi mấy bài này bấm máy tính là ra mà ông
a) \(3x^2+4x=0\Leftrightarrow\left(3x+4\right)x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+4=0\Leftrightarrow x=-\dfrac{4}{3}\end{matrix}\right.\)
➤\(x\in\left\{0;-\dfrac{4}{3}\right\}\)
b) \(-2x^2-8=0\Leftrightarrow-2x^2+\left(-2\right)\cdot4=0\)
\(\Leftrightarrow\left(x^2+4\right)\cdot\left(-2\right)=0\\ \Leftrightarrow x^2+4=0\\\Rightarrow x^2=\varnothing\Leftrightarrow x=\varnothing \)
vì với mọi x, ta luôn đúng với: \(x^2\ge0\Leftrightarrow x^2+4\ge4>0\)
➤\(x=\varnothing\)
c)\(2x^2-7x^2+5=0\)
+) \(a+b+c=2+\left(-7\right)+5=7-7=0\)
Do đó, phương trình có 2 nghiệm sau:
\(x=1\) và \(x=\dfrac{5}{2}=2,5\)
➤\(x\in\left\{1;2,5\right\}\)
d) \(x^2-8x-48=0\)
+)\(\Delta=\left(-8\right)^2-4\cdot1\cdot\left(-48\right)=64+192=266>0\)
\(\Leftrightarrow\sqrt{\Delta}=\sqrt{266}\)
➢Do đó, ta có: \(\left[{}\begin{matrix}x=\dfrac{\sqrt{266}-\left(-8\right)}{2\cdot2}=\dfrac{\sqrt{266}+8}{4}\\x=\dfrac{-\sqrt{266}-\left(-8\right)}{2\cdot2}=\dfrac{8-\sqrt{266}}{4}\end{matrix}\right.\)
➤ \(x\in\left\{\dfrac{8+\sqrt{266}}{4};\dfrac{8-\sqrt{266}}{4}\right\}\)
Bài 1 : giải phương trình
a) (8x + 3)(2x - 1) = (2x - 1)2
b) (x - 5)2 - 36 = 0
c) (4x - 3)2 - 4(x + 3)2
d) x3 - 3x -2 = 0
e) x3 + 2x2 - 4x - 8 = 0
Giải phương trình
a, (x^2-2)(x^2+x+1)=0
b, 16x^2 - 8x + 5=0
c, 2x^3 - x^2 - 8x + 4=0
d, 3x^3+6x^2 - 75x -150 = 0
e, 2x^5-3x^4+6x^3-8x^2+3=0
*vn:vô nghiệm.
a. \(\left(x^2-2\right)\left(x^2+x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2=0\\x^2+x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
-Vậy \(S=\left\{\pm\sqrt{2}\right\}\).
b. \(16x^2-8x+5=0\)
\(\Leftrightarrow16x^2-8x+1+4=0\)
\(\Leftrightarrow\left(4x-1\right)^2+4=0\) (vô lí)
-Vậy S=∅.
c. \(2x^3-x^2-8x+4=0\)
\(\Leftrightarrow x^2\left(2x-1\right)-4\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\pm2\end{matrix}\right.\)
-Vậy \(S=\left\{\dfrac{1}{2};\pm2\right\}\).
d. \(3x^3+6x^2-75x-150=0\)
\(\Leftrightarrow3x^2\left(x+2\right)-75\left(x+2\right)=0\)
\(\Leftrightarrow3\left(x+2\right)\left(x^2-25\right)=0\)
\(\Leftrightarrow3\left(x+2\right)\left(x+5\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\pm5\end{matrix}\right.\)
-Vậy \(S=\left\{-2;\pm5\right\}\)
Giải phương trình bằng cách đặt ẩn phụ:
a ) 2 x 2 − 2 x 2 + 3 x 2 − 2 x + 1 = 0 b ) x + 1 x 2 − 4 ⋅ x + 1 x + 3 = 0
a) 2 x 2 − 2 x 2 + 3 x 2 − 2 x + 1 = 0 ( 1 )
Đặt x 2 – 2 x = t ,
(1) trở thành : 2 t 2 + 3 t + 1 = 0 ( 2 ) .
Giải (2) :
Có a = 2 ; b = 3 ; c = 1
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = - 1 / 2 .
+ Với t = -1 ⇒ x 2 − 2 x = − 1 ⇔ x 2 − 2 x + 1 = 0 ⇔ ( x − 1 ) 2 = 0 ⇔ x = 1
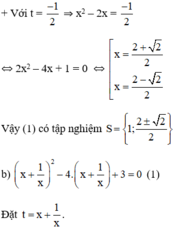
(1) trở thành: t 2 – 4 t + 3 = 0 ( 2 )
Giải (2):
Có a = 1; b = -4; c = 3
⇒ a + b + c = 0
⇒ (2) có nghiệm t 1 = 1 ; t 2 = c / a = 3 .
+ t = 1 ⇒ x + 1/x = 1 ⇔ x 2 + 1 = x ⇔ x 2 – x + 1 = 0
Có a = 1; b = -1; c = 1 ⇒ Δ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
Phương trình vô nghiệm.

Giải phương trình bằng cách đưa về phương trình tích:
a ) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0 b ) x 3 + 3 x 2 − 2 x − 6 = 0 c ) x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x d ) x 2 + 2 x − 5 2 = x 2 − x + 5 2
a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
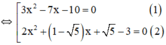
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
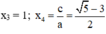
Vậy phương trình có tập nghiệm 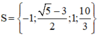
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
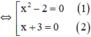
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
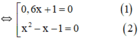
+ Giải (1): 0,6x + 1 = 0 ⇔ 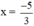
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 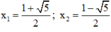
Vậy phương trình có tập nghiệm 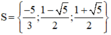
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
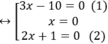
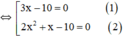
+ Giải (1): 3x – 10 = 0 ⇔ 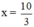
+ Giải (2):
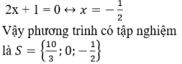
Giải bất phương trình
a, (5x-1)(x-3) < 0
b, (2x+3)(3-5x)(x-2) > 0
c, \(\dfrac{4x+1}{2x-5}_{ }\le\) 0
d, B= |x+2|+|3-x|
a) Ta có: (5x-1)(x-3)<0
nên 5x-1 và x-3 trái dấu
Trường hợp 1:
\(\left\{{}\begin{matrix}5x-1>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{1}{5}\\x< 3\end{matrix}\right.\Leftrightarrow\dfrac{1}{5}< x< 3\)
Trường hợp 2:
\(\left\{{}\begin{matrix}5x-1< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{1}{5}\\x>3\end{matrix}\right.\Leftrightarrow loại\)
Vậy: S={x|\(\dfrac{1}{5}< x< 3\)}