vì xoy và yoz là 2 góc kề bù =>xoz=180^o

mà xoy-yoz=40^o (dạng toán tổng hiệu)

xoy= (xoz+40^o):2=(180+40):2=110^o

yoz=180-110=70^o

cảm ơn bạn

ko có j

Ta có \(\widehat{MON}=\widehat{yOM}+\widehat{yON}=\dfrac{1}{2}\widehat{xOy}+\dfrac{1}{2}\widehat{yOz}=\dfrac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\dfrac{1}{2}\cdot180=90\)

Vậy ...

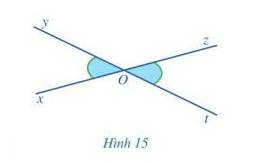
a) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz nằm về hai phía đối với đường thẳng chứa tia Oy nên hai góc xOy và yOz là hai góc kề nhau. Hơn nữa, hai góc xOy và yOz có tổng bằng góc xOz =180 độ nên hai góc xOy và yOz là hai góc bù nhau.

Vậy hai góc xOy và yOz là hai góc kề bù

Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz là hai tia đối nhau nên hai góc xOy và yOz là hai góc kề bù.

b) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot nằm về hai phía đối với đường thẳng chứa tia Oz nên hai góc yOz và zOt là hai góc kề nhau. Hơn nữa, hai góc yOz và zOt có tổng bằng góc xOz =180 độ nên hai góc yOz và zOt là hai góc bù nhau.

Vậy hai góc yOz và zOt là hai góc kề bù

Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot là hai tia đối nhau nên hai góc yOz và zOt là hai góc kề bù.

c) Do

\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = \widehat {xOz} = 180^\circ ;\\\widehat {yOz} + \widehat {zOt} = \widehat {yOt} = 180^\circ \end{array}\)

Vậy \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\)

\( \Rightarrow \widehat {xOy} = \widehat {zOt}\)

Chú ý: Ta có thể dùng dấu hiệu sau: 2 góc kề bù khi có chung đỉnh, chung một cạnh, 2 cạnh còn lại là 2 tia đối nhau.

vì xOy và yOz là hai góc kề bù

=> xOy + yOz = 180 độ

Mà yOz = 1/5 xOy

Thay vào , ta được :

xOy + 1/5 xOy = 180 độ

xOy . ( 1 + 1/5 ) = 180 độ

xOy . 6/5 = 180 độ

xOy = 180 độ : 6/5

xOy = 150