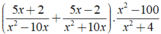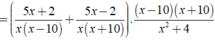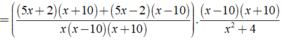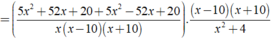\(\frac{x^4-5x^2+4}{x^4-10x^2+9}\)    \(ĐKXĐ:x\ne\pm3\)

\(=\frac{x^4-4x^2-x^2+4}{x^4-9x^2-x^2+9}\)

\(=\frac{\left(x^4-4x^2\right)-\left(x^2-4\right)}{\left(x^4-9x^2\right)-\left(x^2-9\right)}\)

\(=\frac{x^2.\left(x^2-4\right)-\left(x^2-4\right)}{x^2.\left(x^2-9\right)-\left(x^2-9\right)}\)

\(=\frac{\left(x^2-1\right)\left(x^2-4\right)}{\left(x^2-1\right)\left(x^2-9\right)}\)

\(=\frac{x^2-4}{x^2-9}\)    

\(\frac{x^4-5x^2+4}{x^4-10x^2+9}=\frac{x^4-x^2-4x^2+4}{x^4-x^2-9x^2+9}=\frac{x^2.\left(x^2-1\right)-4.\left(x^2-1\right)}{x^2.\left(x^2-1\right)-9.\left(x^2-1\right)}\)

                                                                           \(=\frac{\left(x^2-4\right)\left(x^2-1\right)}{\left(x^2-1\right)\left(x^2-9\right)}=\frac{x^2-4}{x^2-9}\)

Lời giải:

a. ĐKXĐ: $x\neq \pm 1; \pm 3$

$A=\frac{x^4-5x^2+4}{x^4-10x^2+9}=\frac{(x-1)(x+1)(x-2)(x+2)}{(x-1)(x+1)(x-3)(x+3)}$

$=\frac{(x-2)(x+2)}{(x-3)(x+3)}=\frac{x^2-4}{x^2-9}$
b.

Để $A=0$ thì $x^2-4=0$

$\Leftrightarrow (x-2)(x+2)=0$

$\Leftrightarrow x=\pm 2$ (thỏa mãn) 

c.

$|2x-1|=7$

$\Rightarrow 2x-1=7$ hoặc $2x-1=-7$

$\Rightarrow x=4$ hoặc $x=-3$.

Mà $x\neq \pm 1; \pm 3$ nên $x=4$

Khi đó:

$A=\frac{4^2-4}{4^2-9}=\frac{12}{7}$

\(P=\dfrac{15x^5y^3-10x^3y^2+20x^4y^4}{5x^2y^2}\)

\(=\dfrac{15x^5y^3}{5x^2y^2}-\dfrac{10x^3y^2}{5x^2y^2}+\dfrac{20x^4y^4}{5x^2y^2}\)

\(=3x^3y-2x+4x^2y^2\)

Khi x=-1 và y=2 thì \(P=3\cdot\left(-1\right)^3\cdot2-2\cdot\left(-1\right)+4\cdot\left(-1\right)^2\cdot2^2\)

\(=-6+2+16=4+16=20\)

\(x\ge-\dfrac{4}{5}\)

\(A=5x+2+\left|5x+4\right|=5x+2+5x+4=10x+6\)

\(x< -\dfrac{4}{5}\)

\(A=5x+2+\left|5x+4\right|=5x+2-5x+4=6\)

1.

\(A=\dfrac{2x-9}{\left(x-2\right)\left(x-3\right)}-\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-2\right)\left(x-3\right)}+\dfrac{\left(2x+4\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\)

\(=\dfrac{2x-9-\left(x^2-9\right)+\left(2x^2-8\right)}{\left(x-2\right)\left(x-3\right)}\)

\(=\dfrac{x^2+2x-8}{\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x-2\right)\left(x+4\right)}{\left(x-2\right)\left(x-3\right)}\)

\(=\dfrac{x+4}{x-3}\)

b.

\(A=2\Rightarrow\dfrac{x+4}{x-3}=2\Rightarrow x+4=2\left(x-3\right)\)

\(\Rightarrow x=10\) (thỏa mãn)

2.

\(x^4+2x^2y+y^2-9=\left(x^2+y\right)^2-3^2=\left(x^2+y-3\right)\left(x^2+y+3\right)\)

1:

a: \(\left(2x-5\right)^2-4x\left(x+3\right)\)

\(=4x^2-20x+25-4x^2-12x\)

=-32x+25

b: \(\left(x-2\right)^3-6\left(x+4\right)\left(x-4\right)-\left(x-2\right)\left(x^2+2x+4\right)\)

\(=x^3-6x^2+12x-8-\left(x^3-8\right)-6\left(x^2-16\right)\)

\(=-6x^2+12x-6x^2+96=-12x^2+12x+96\)

c: \(\left(x-1\right)^2-2\left(x-1\right)\left(x+2\right)+\left(x+2\right)^2+5\left(2x-3\right)\)

\(=\left(x-1-x-2\right)^2+5\left(2x-3\right)\)

\(=\left(-3\right)^2+5\left(2x-3\right)\)

\(=9+10x-15=10x-6\)

2: 

a: \(\left(2-3x\right)^2-5x\left(x-4\right)+4\left(x-1\right)\)

\(=9x^2-12x+4-5x^2+20x+4x-4\)

\(=4x^2+12x\)

b: \(\left(3-x\right)\left(x^2+3x+9\right)+\left(x-3\right)^3\)

\(=27-x^3+x^3-9x^2+27x-27\)

\(=-9x^2+27x\)

c: \(\left(x-4\right)^2\left(x+4\right)-\left(x-4\right)\left(x+4\right)^2+3\left(x^2-16\right)\)

\(=\left(x-4\right)\left(x+4\right)\left(x-4-x-4\right)+3\left(x^2-16\right)\)

\(=\left(x^2-16\right)\left(-8\right)+3\left(x^2-16\right)\)

\(=-5\left(x^2-16\right)=-5x^2+80\)

`1)` Biểu thức xác định `<=>x+1 \ne 0<=>x \ne -1`

`[x^2+2x+1]/[x+1]=[(x+1)^2]/[x+1]=x+1`

`2)` Bth xác định `<=>x(x-3) \ne 0<=>{(x \ne 0),(x \ne 3):}`

`[x^2-6x+9]/[x(x-3)]=[(x-3)^]/[x(x-3)]=[x-3]/x`

`3)` Bth xác định `<=>2x(x+2) \ne 0<=>{(x \ne 0),(x \ne -2):}`

`[x^2-4]/[2x(x+2)]=[(x-2)(x+2)]/[2x(x+2)]=[x-2]/[2x]`

`4)` Bth xác định `<=>5x^2-10x \ne 0<=>5x(x-2) \ne 0<=>{(x \ne 0),(x \ne 2):}`

`[x^2-2x]/[5x^2-10x]=[x(x-2)]/[5x(x-2)]=1/5`

1)

\(ĐKXĐ:x\ne-1\)

\(\dfrac{x^2+2x+1}{x+1}\\ =\dfrac{\left(x+1\right)^2}{x+1}\\ =x+1\)

2)

ĐKXĐ x khác 0 và x khác 3

\(\dfrac{x^2-6x+9}{x\left(x-3\right)}\\ =\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}\\ =\dfrac{x-3}{x}\)

3)

ĐKXĐ: x khác 0 và x khác -2

\(\dfrac{x^2-4}{2x\left(x+2\right)}\\ =\dfrac{\left(x-2\right)\left(x+2\right)}{2x\left(x+2\right)}\\ =\dfrac{x-2}{2x}\)

4)

DKXĐ: x khác 0 và x khác 2

\(\dfrac{x^2-2x}{5x^2-10x}\\ =\dfrac{x\left(x-2\right)}{5x\left(x-2\right)}\\ =\dfrac{1}{5}\)

đk `x≠-1`

`(x^2+2x+1)/(x+1)`

`=((x+1)^2)/(x+1)`

`=x+1`

---------

đk \(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne3\end{matrix}\right.\)

`(x^2-6x+9)/(x(x-3))`

`=((x-3)^2)/(x(x-3))`

`=(x-3)/x`

--------

 đk \(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne-2\end{matrix}\right.\)

`(x^2-4)/(2x(x+2))`

`=((x-2)(x+2))/(2x(x+2))`

`=(x-2)/(2x)`

--------

đk \(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)

`(x^2-2x)/(5x^2-10x)`

`=(x(x-2))/(5x(x-2))`

`=x/(5x)`

Ta có: 

Vậy  A   =   10 x