b: Phương trình hoành độ giao điểm là:

\(x^2+\left(m-2\right)x-m^2-1=0\)

\(ac=-m^2-1< 0\)

Do đó: (P) luôn cắt (d) tại hai điểm phân biệt

b) Phương trình hoành độ giao điểm của (P) và (d) là:

- x 2  = 2mx - 5 ⇔  x 2  + 2mx - 5 = 0

Δ'= m 2 + 5 > 0 với ∀m ∈ R

Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.

Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:

- x 2 = 4x - 5 ⇔ x 2  + 4x - 5 = 0

Δ = 4 2  - 4.1.(-5) = 36

⇒ Phương trình có 2 nghiệm

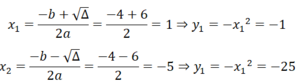
Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)

1: Điểm cố định của (d) là:

x=0 và y=m*0+2=2

2: PTHĐGĐ là:

x2-mx-2=0

a=1; b=-m; c=-2

Vì a*c<0

nên (P) luôn cắt (d) tại hai điểm khác phía so với trục tung

a) Để (d) đi qua điểm A(1;3) thì \(3=2m.1+5\Rightarrow2m=-2\Rightarrow m=-1\)

b) Xét phương trình hoành độ giao điểm: \(x^2=2mx+5\)

\(\Rightarrow x^2-2mx-5=0\left(I\right)\)

Ta có \(\Delta'=m^2+5>0,\forall m\) nên PT (I) luôn có 2 nghiệm phân biệt \(x_1,x_2\) với mọi \(m\)

Vậy (d) luôn cắt (P) tại hai điểm phân biệt.

c) Áp dụng hệ thức Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-5\end{matrix}\right.\)

Để \(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)

\(\Leftrightarrow4m^2-2.\left(-5\right)=4\Leftrightarrow4m^2=-6\) (Vô lý)

Vậy không có m thỏa mãn ycbt.

b) Phương trình hoành độ giao điểm của d và (P):  − x 2 = 2 m x − 1 ⇔ x 2 + 2 m x − 1 = 0

Phương trình (*) có ∆’ = m² + 1 > 0 ⇒ (*) luôn có hai nghiệm phân biệt x₁, x₂ ∀ m hay d luôn cắt (P) tại hai điểm phân biệt.

Áp dụng Viét ta có  x 1 + x 2 = − 2 m x 1 x 2 = − 1 ⇒ | x 1 − x 2 | = ( x 1 − x 2 ) 2 = ( x 1 + x 2 ) 2 − 4 x 1 x 2 = 4 m 2 + 4 = 2 m 2 + 1

Khi đó ta có 

y 1 = 2 m x 1 − 1 y 2 = 2 m x 2 − 1 ⇒ | y 1 2 − y 2 2 | = | ( 2 m x 1 − 1 ) 2 − ( 2 m x 2 − 1 ) 2 | ⇒ | y 1 2 − y 2 2 | = | ( 2 m x 1 − 1 − 2 m x 2 + 1 ) ( 2 m x 1 − 1 + 2 m x 2 − 1 ) | = | 4 m ( x 1 − x 2 ) [ m ( x 1 + x 2 ) − 1 ] | = | 4 m ( 2 m 2 + 1 ) ( x 1 − x 2 ) | = 4 m ( 2 m 2 + 1 ) | x 1 − x 2 | = 4 | m | ( 2 m 2 + 1 ) 2 m 2 + 1 Ta có:  | y 1 2 − y 2 2 | = 3 5 ⇔ 64 m 2 ( 2 m 2 + 1 ) 2 ( m 2 + 1 ) = 45 ⇔ 64 ( 4 m 4 + 4 m 2 + 1 ) ( m 4 + m 2 ) = 45

Đặt: m 4 + m 2 = t ≥ 0   có phương trình  64 t ( 4 t + 1 ) = 45 ⇔ 256 t 2 + 64 t − 45 = 0 ⇔ t = 5 16   ( v ì   t ≥ 0 ) ⇒ m 4 + m 2 = 5 16 ⇔ 16 m 4 + 16 m 2 − 5 = 0 ⇔ m = ± 1 2

Vậy  m = ± 1 2

- Xét phương trình hoành độ giao điểm : \(x^2=2mx-2m+3\)

\(\Leftrightarrow x^2-2mx+2m-3=0\left(I\right)\)

- Xét thấy để P và d cắt nhau tại hai điểm phân biệt khi PT ( I ) có hai nghiệm phân biệt .

\(\Leftrightarrow\Delta^,=b^{,2}-ac=m^2-\left(2m-3\right)>0\)

\(\Leftrightarrow m^2-2m+3>0\)

Mà \(m^2-2m+3=m^2-2m+1+2=\left(m+1\right)^2+2\ge2>0\forall m\in R\)

Vậy ... ĐPCM

a: PTHĐGĐ là;

x^2-(2m-3)x+m^2-3m=0

Δ=4m^2-12m+9-4m^2+12m=9>0

=>(P) luôn cắt (d) tại hai điểm pb

b: |x1|+|x2|=3

=>x1^2+x2^2+2|x1x2|=9

=>(2m-3)^2-2(m^2-3m)+2|m^2-3m|=9

TH1: m>=3 hoặc m<=0

=>(2m-3)^2=9

=>m=3(nhận) hoặc m=0(nhận)

Th2: 0<m<3

=>4m^2-12m+9-4(m^2-3m)=9

=>4m^2-12m-4m^2+12m=0

=>0m=0(luôn đúng)