Tìm giá trị lớn nhất của hàm số  trên đoạn [-1,2]
trên đoạn [-1,2]
A.21 B.-2 C.-1 D.1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = -x2 + 4x - 5 đạt cực đại tại đỉnh (2; -1). Vì vậy GTLN của hàm số trên đoạn [0;3] là y(2) = -1
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = - x 2 + 4x - 5 đạt cực đạt tại đỉnh (2; -1). Vì vậy giá trị lớn nhất của hàm số trên đoạn [0;3] là y(2) = -1.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng
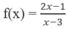
A. 1/3 và -3 B. 3/2 và -1
C. 2 và -3 D. 1/2 và 5
Đáp án: A.
Tập xác định: D = R \{3}
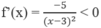 ∀x ∈ D.
∀x ∈ D.
Do đó f(x) nghịch biến trên (- ∞ ; 3) và (3; + ∞ ).
Ta thấy [0;2] ⊂ (- ∞ ;3). Vì vậy
max f(x) = f(0) = 1/3, min f(x) = f(2) = -3.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng
f x = 2 x - 1 x - 3
A. 1/3 và -3 B. 3/2 và -1
C. 2 và -3 D. 1/2 và 5
Đáp án: A.
Tập xác định: D = R \{3}
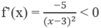 ∀
x
∈
D.
∀
x
∈
D.
Do đó f(x) nghịch biến trên (- ∞ ; 3) và (3; + ∞ ).
Ta thấy [0;2] ⊂ (- ∞ ;3). Vì vậy
max f(x) = f(0) = 1/3, min f(x) = f(2) = -3.
Cho hàm số \(y=\sqrt{x-1}+x^2-2x\)
a, Xét sự biến thiên của hàm số đã cho trên [ 1;+\(\infty\))
b, Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn \(\left[2;5\right]\)
please help me
i need it now
Cho hàm số f(x) = x - 1 2 a x 2 + 4 a x - a + b - 2 , với a,b ∈ ℝ . Biết trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1. Hỏi trên đoạn - 2 ; - 5 4 , hàm số đạt giá trị nhỏ nhất tại giá trị nào của x?
A. x = - 5 4
B. x = - 4 3
C. x = - 3 2
D. x = -2
Chọn C
Tập xác định của hàm số là ℝ .
Ta có: ![]()
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
![]()
![]()
![]()
Khi đó f'(x) = 0 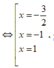 ( đều là các nghiệm đơn)
( đều là các nghiệm đơn)
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
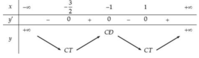
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4
Giá trị lớn nhất của hàm số y = 2 x 3 + 3 x 2 − 12 x + 2 trên đoạn − 1,2 là
A. 15
B. 66
C. 11
D. 10
Đáp án A
Giải:
TXĐ: D = ℝ .
f ' x = 6 x 2 + 6 x − 12
f ' x = 0 ⇔ x = 1 ∈ − 1 ; 2 x = − 2 ∉ − 1 ; 2
Ta có f − 1 = 15 , f 1 = − 5 , f 2 = 6 .
Do f liên tục trên − 1 ; 2 nên suy ra max x ∈ − 1 ; 2 f x = 15.
Giá trị lớn nhất của hàm số y = 2 x 3 + 3 x 2 − 12 x + 2 trên đoạn − 1,2 là
A. 15
B. 66
C. 11
D. 10
Đáp án A
TXĐ D = ℝ
f ' x = 6 x 2 + 6 x − 12 f ' x = 0 ⇔ x = 1 ∈ − 1 ; 2 x = − 2 ∉ − 1 ; 2
ta có f − 1 = 15 , f 1 = − 5 , f 2 = 6
Do f liên tục trên − 1 ; 2 nên suy ra max x ∈ − 1 ; 2 f x = 15.