Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đểu ba cạnh của tam giác ABC
a) Chứng minh: Tam giác ABD= tam giác ACD
b) So sánh DBC và DCB
c) chứng minh: AD đi qua trung điểm M của BC.
d) chứng minh ba điểm A,G,I thẳng hàng
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
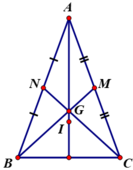
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà 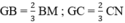 (Tính chất trọng tâm của tam giác)
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
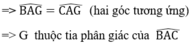
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của 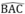
Vì G, I cùng thuộc tia phân giác của 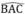 nên A, G, I thẳng hàng
nên A, G, I thẳng hàng
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Gọi giao điểm của BG với AC là M ;
CG với AB là N
Vì G là trọng tâm của \(\Delta ABC\)
nên BM, CN, là trung tuyến
Mặt khác \(\Delta ABC\) cân tại A
Nên BM = CN
Ta có : \(GB=\frac{1}{2}BM;GC=\frac{2}{3}CN\) (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó : \(\Delta AGB=\Delta AGC\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\Rightarrow G\) thuộc phân giác của \(\widehat{BAC}\)
Mà \(\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\Rightarrow I\) thuộc phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc phân giác của \(\widehat{BAC}\) nên A, G, I thẳng hàng
Chúc bạn học tốt !!!
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Giải
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà \(GB=\frac{2}{3}BM;GC=\frac{2}{3}CN\)(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\)( hai góc tương ứng )
\(\Rightarrow\)G là trọng tâm của \(\widehat{BAC}\)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc tia phân giác của \(\widehat{BAC}\)nên A, G, I thẳng hàng
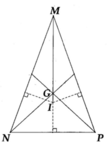
Cho tam giác MNP cân tại M có G là trọng tâm I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm M, G, I thẳng hàng.
I nằm trong tam giác và cách đều ba cạnh của tam giác nên MI là tia phân giác của góc M.
Do tam giác MNP cân tại M nên đường giác MI cũng là đường trưng tuyến.
G là trọng tâm của tam giác MNP nên G nằm trên MI.
Từ đó, suy ra M,G, I thẳng hàng.
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh điểm A, G, I thẳng hàng ?

Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng
Hướng dẫn:
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
ˆBAD=ˆCADBAD^=CAD^
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> ˆDBC=ˆDCB
Hướng dẫn:

Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = 1212BM; GC = 2323CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> ˆBAG=ˆCAGBAG^=CAG^ => G thuộc phân giác của ˆBACBAC^
Mà ∆ABI = ∆ACI (c.c.c)
=> ˆBAI=ˆCAIBAI^=CAI^ => I thuộc phân giác của ˆBACBAC^
Vì G, I cùng thuộc phân giác của ˆBACBAC^ nên A, G, I thẳng hàng
Cho tam giác ABC cân Tại A . Gọi G là Trọng Tâm I Là Điểm Nằm Trong Tam Giác Và Cách Đều Ba Cạnh Của Tam Giác Đó . Chứng Minh Ba Điểm A , G , I Thẳng Hàng .
Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng
Vì G là trọng tâm của tam giác ABC trên D thuộc đường trung tuyến AM (1)
Vì I là giao điểm các phân giác của tam giác ABC nên AI là tia phân giác của góc A mà trong tam giác cân phân giác của góc ở đỉnh của tam giác cũng là trung tuyến do đó I thuộc trực tuyến AM(2)
Từ (1) và (2 )suy ra 3 điểm A,I,G thẳng hàng
G là trọng tâm của ΔABCΔABC nên G thuộc đường trung tuyến AM (1)
Trong tam giác cân, đường trung phân giác của góc ở đỉnh đồng thời là đường trung tuyến nên I cũng thuộc đường trung tuyến AM. (2)
Từ (1) và (2) suy ra A, G, I thẳng hàng.
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó . Chứng minh ba điểm A,G,I thẳng hàng
Cho tam giác ABC cân tại A. gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng
Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng
Cho tam giác ABC cân tại A. gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng
Đe ma ban .vi G la trong tam nen AG la duong trung tuyen cua tam giac ABC ma tam giac ABC can nen dong thoi la duong phan giac.MATkhac I cach deu 3 canh nen ai la duong phan giac.dan den A,G,I thang hang