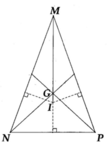
I nằm trong tam giác và cách đều ba cạnh của tam giác nên MI là tia phân giác của góc M.
Do tam giác MNP cân tại M nên đường giác MI cũng là đường trưng tuyến.
G là trọng tâm của tam giác MNP nên G nằm trên MI.
Từ đó, suy ra M,G, I thẳng hàng.
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Cho tam giác ABC cân Tại A . Gọi G là Trọng Tâm I Là Điểm Nằm Trong Tam Giác Và Cách Đều Ba Cạnh Của Tam Giác Đó . Chứng Minh Ba Điểm A , G , I Thẳng Hàng .
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó . Chứng minh ba điểm A,G,I thẳng hàng
Cho tam giác ABC cân tại A. gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng
Cho tam giác ABC cân tại A. gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I nằm trong tam giác va cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A,G,I thẳng hàng
cho tam giác ABC cân tại .gọi G là trọng tâm,I là điểm nằm trong tam giác và cách đều 3 cạnh của tam giác đó.Chứng minh ba điểm A,G,I thẳng hàng
cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh :
a/ Ba điểm A,G,| thẳng hàng
b/ BG<BI<BA
c/ Góc IBG= góc ICG
d/ Xác đinh vị trí của điểm M sao cho tổng độ dài BM+MC có giá trị nhỏ nhất
